题目内容

已知椭圆
x2
10-m
+
y2
m-4
=1的长轴在y轴上，且焦距为2，则m等于（　　）
A、9B、8C、7.5D、7
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据条件可得a2=m-4，b2=10-m，c2=a2-b2=2m-14．由焦距为2，即c=1．即可得到m的值．
解答： 解：由椭圆
x2
10-m
+
y2
m-4
=1的长轴在y轴上，
则a2=m-4，b2=10-m，c2=a2-b2=2m-14．
由焦距为2，即2c=2，即有c=1．
即有2m-14=1，解得m=7.5．
故选C．
点评：本题考查椭圆的方程和性质，考查椭圆中的参数a，b，c的关系，属于基础题．
练习册系列答案
相关题目
已知{an}是各项为正数的等差数列，a1，a2，a4成等比数列．令bn=
1
a2n
，n=1，2，3…．
（1）证明{bn}为等比数列；
（2）如果无穷数列{bn}各项的和S=
1
3
，求数列{an}的首项a1和公差d；
（3）在（2）的条件下令cn=an+1，是否存在m，k∈N，有cm+cm+1=ck？说明理由．
已知双曲线
x2
10-m
+
y2
m-2
=1的实轴在y轴上且焦距为8，则双曲线的渐近线方程为
 
．
已知数列{an}满足a1=
1
4
，an=
an-1
(-1)nan-1-2
（n≥2，n∈N*）．
（1）证明数列{
1
an
+(-1)n}为等比数列，并求数列{an}的通项公式；
（2）设bn=
1
an2
，求{bn}的前n项和Sn；
（3）设cn=ansin
(2n-1)π
2
，数列{cn}的前n项和Tn，求证：对?n∈N*，Tn＜
4
7
．
一个多面体的直观图（图1）及三视图（图2）如图所示，其中M，N分别是AF、BC的中点
（Ⅰ）求证：MN∥平面CDEF：
（Ⅱ）求二面角A-CF-B的余弦值；
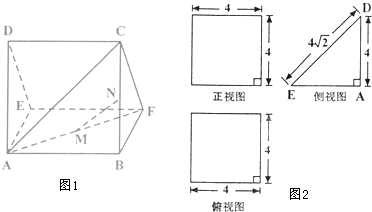
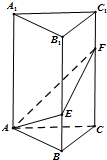如图，在直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=2，AA1=6，点E、F分别在棱BB1、CC1上，且BE=
1
3
BB1，C1F=
1
3
CC1．
（1）求异面直线AE与A1 F所成角的大小；
（2）求平面AEF与平面ABC所成角的余弦值．
已知x，y满足不等式组
y≤x
x+y≥2
x≤2
，则目标函数z=2x+y的最大值为
 
．
已知函数f（x）=-
1
2
+
1
2x+1
． 
（1）证明：函数f（x）是减函数；   
（2）证明：函数f（x）是奇函数．
下面四个条件中，使a＞b成立的充分不必要条件是（　　）
A、a3＞b3
B、a＞b+1
C、a2＞b2
D、a＞b-1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网