题目内容
设全集U=R,A={x||x+1|<1},B={x|(
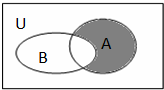
)x-2≥0},则图中阴影部分所表示的集合( )
| 1 |
| 2 |

| A、(-2,0) |
| B、(-2,-1] |
| C、(-1,0] |
| D、(-1,0) |
考点:Venn图表达集合的关系及运算
专题:集合
分析:由图象可知阴影部分对应的集合为A∩(∁UB),然后根据集合的基本运算求解即可.
解答:
解:由Venn图可知阴影部分对应的集合为A∩(∁UB),
∵A={x||x+1|<1}={x|-2<x<0},B={x|(
)x-2≥0}={x|x≤-1},
∴∁UB={x|x>-1},
即A∩(∁UB)={x|-1<x<0},
故选:D
∵A={x||x+1|<1}={x|-2<x<0},B={x|(
| 1 |
| 2 |
∴∁UB={x|x>-1},
即A∩(∁UB)={x|-1<x<0},
故选:D
点评:本题主要考查集合的基本运算,利用图象先确定集合关系是解决本题的关键,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
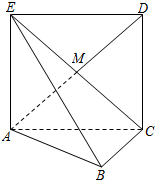 如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC.
如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC.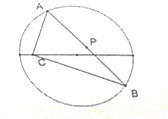 已知x2+y2=a2,定点C(c,0).(a>0,c≠a).AB为圆上的动点∠ACB=90°.求AB中点P的轨迹方程.
已知x2+y2=a2,定点C(c,0).(a>0,c≠a).AB为圆上的动点∠ACB=90°.求AB中点P的轨迹方程.