题目内容
弧长为3π，圆心角为
π的扇形的面积为 ．
| 3 |
| 4 |
考点：扇形面积公式
专题：计算题,三角函数的求值
分析：根据扇形面积公式，则必须知道扇形所在圆的半径，设其半径是r，则其弧长是
πr，再根据弧长是3π，列方程求解．
| 3 |
| 4 |
解答：
解：设扇形的半径是r，根据题意，得：
πr=3π，
解，得r=4．
则扇形面积是
×3π×4=6π．
故答案为：6π．
| 3 |
| 4 |
解，得r=4．
则扇形面积是
| 1 |
| 2 |
故答案为：6π．
点评：此题考查了扇形的面积公式以及弧长公式，求出扇形的半径是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若定义在R上的可导函数y=f（x）满足f（1+x）=f（1-x），且（x-1）f′（x）＜0（x≠1），则“对于任意的x1＜x2，都有f（x1）＞f（x2）”是“x1+x2＞2”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
“a＞2”是“函数y=ax是增函数”的（ ）
| A、充分必要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
若定义在R上的函数f（x）满足f（x1+x2）=f（x1）+f（x2），则函数f（x）一定是（ ）
| A、奇函数 | B、偶函数 |
| C、减函数 | D、增函数 |
已知原命题：若a+b＞2，则a，b至少有一个大于1，那么原命题与其逆命题的真假情况是（ ）
| A、原命题真，逆命题假 |
| B、原命题假，逆命题真 |
| C、原命题与逆命题均为真命题 |
| D、原命题与逆命题均为假命题 |
命题“x＞y”，则x2＞y2的逆否命题是（ ）
| A、若x≤y，则x2≤y2 |
| B、若x2≤y2，则x＞y |
| C、若x2＞y2，则x≥y |
| D、若x2≤y2，则x≤y |
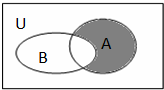
设全集U=R，A={x||x+1|＜1}，B={x|（
）x-2≥0}，则图中阴影部分所表示的集合（ ）
| 1 |
| 2 |
| A、（-2，0） |
| B、（-2，-1] |
| C、（-1，0] |
| D、（-1，0） |