题目内容
已知函数y=f（x）的图象在点M（1，f（1））处的切线方程是y=x+3，则f（1）+f′（1）= ．
考点：导数的运算,导数的几何意义
专题：导数的概念及应用
分析：根据导数的几何意义和切线方程可求出f（1）、f′（1），代入f（1）+f′（1）求值即可．
解答：
解：由题意值，y=f（x）的图象在点M（1，f（1））处的切线方程是y=x+3，
由导数的几何意义得f′（1）=1，且f（1）=4，
所以f（1）+f′（1）=5，
故答案为：5．
由导数的几何意义得f′（1）=1，且f（1）=4，
所以f（1）+f′（1）=5，
故答案为：5．
点评：本题考查导数的几何意义，以及切线方程的应用，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若定义在R上的可导函数y=f（x）满足f（1+x）=f（1-x），且（x-1）f′（x）＜0（x≠1），则“对于任意的x1＜x2，都有f（x1）＞f（x2）”是“x1+x2＞2”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知x＞0，则y=x+
+1的最小值是（ ）
| 1 |
| x |
| A、2 | B、3 | C、4 | D、6 |
已知向量
=（2，1），
=（-1，k2-2），则k=2是
⊥
的（ ）
| a |
| b |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
“a＞2”是“函数y=ax是增函数”的（ ）
| A、充分必要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
若定义在R上的函数f（x）满足f（x1+x2）=f（x1）+f（x2），则函数f（x）一定是（ ）
| A、奇函数 | B、偶函数 |
| C、减函数 | D、增函数 |
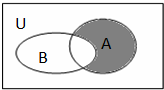
设全集U=R，A={x||x+1|＜1}，B={x|（
）x-2≥0}，则图中阴影部分所表示的集合（ ）
| 1 |
| 2 |
| A、（-2，0） |
| B、（-2，-1] |
| C、（-1，0] |
| D、（-1，0） |