题目内容
10.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为$\sqrt{3}$,实轴长为2,直线l:x-y+m=0与双曲线C交于不同的两点A,B,(1)求双曲线C的方程;
(2)若线段AB的中点在圆x2+y2=5上,求m的值;
(3)若线段AB的长度为4$\sqrt{5}$,求直线l的方程.
分析 (1)根据双曲线的离心率和和实轴长即可求出a,b的值,问题得以解决,
(2)设A、B两点的坐标分别为(x1,y1),(x2,y2),线段AB的中点为M(x0,y0),根据点M(x0,y0)在圆x2+y2=5上,即可求出m的值,
(3)根据弦长公式即可求出m的值.
解答 解:(1)由题意,得$\frac{c}{a}$=$\sqrt{3}$,2a=2,又因为c2=a2+b2
解得a=1,c=$\sqrt{3}$,
∴b2=c2-a2=2
∴所求双曲线C的方程为x2-$\frac{{y}^{2}}{2}$=1.
(2)设A、B两点的坐标分别为(x1,y1),(x2,y2),线段AB的中点为M(x0,y0),
由$\left\{\begin{array}{l}{{x}^{2}-\frac{{y}^{2}}{2}=1}\\{x+y+m=0}\end{array}\right.$得x2-2mx-m2-2=0,判别式△>0,
∴x0=$\frac{{x}_{1}+{x}_{2}}{2}$=m,y0=x0+m=2m,
∵点M(x0,y0)在圆x2+y2=5上,
∴m2+(2m)2=5,
∴m=±1.
(3)由$|{AB}|=\sqrt{{{({x_1}-{x_2})}^2}+{{({y_1}-{y_2})}^2}}$=$\sqrt{{{({x_1}-{x_2})}^2}+{{({x_1}-{x_2})}^2}}$=$\sqrt{2{{({x_1}-{x_2})}^2}}$=$\sqrt{2[{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}$=$\sqrt{2[{{(2m)}^2}-4(-{m^2}-2)}]$=$4\sqrt{5}$
解得m=±2
所以直线l的方程为x-y+2=0或x-y-2=0
点评 本题考查了双曲线的性质和点和圆的位置关系和弦长公式,属于中档题

| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
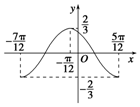
| A. | y=$\frac{2}{3}$sin(2x+$\frac{π}{3}$) | B. | y=$\frac{2}{3}$sin($\frac{x}{2}$+$\frac{π}{4}$) | C. | y=$\frac{2}{3}$sin(x-$\frac{π}{3}$) | D. | y=$\frac{2}{3}$sin(2x+$\frac{2}{3}$π) |
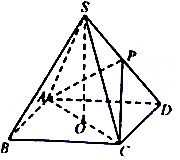 如图,在四棱锥S-ABCD中,点O是正方形ABCD的中心,SO⊥平面ABCD,且SO=OD,点P为棱SD上一点.
如图,在四棱锥S-ABCD中,点O是正方形ABCD的中心,SO⊥平面ABCD,且SO=OD,点P为棱SD上一点.