题目内容
11．已知命题p：方程$\frac{x^2}{t+2}+\frac{y^2}{t-10}=1$表示双曲线；命题q：-m＜t＜m+1（m＞0）． 若q是p的充分非必要条件，试求实数m的取值范围．分析 若q是p的充分非必要条件，则$\left\{\begin{array}{l}-m≥-2\\ m+1≤10\end{array}\right.$，结合m＞0，可得答案．
解答 （本小题10分）
解：若p真，则（t+2）（t-10）＜0，
所以-2＜t＜10…（5分）
因为q是p的充分非必要条件，
所以$\left\{\begin{array}{l}-m≥-2\\ m+1≤10\end{array}\right.$，
又因为m＞0，
∴0＜m≤2…（10分）
点评 本题以命题的真假判断与应用为载体，考查了双曲线的标准方程，充要条件，难度中档．
练习册系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
3．设曲线l极坐标方程为ρcosθ-ρsinθ+1=0，曲线C的参数方程为$\left\{\begin{array}{l}x=\sqrt{2}cosθ\\ y=\sqrt{2}sinθ\end{array}\right.（θ为参数）$，A，B为曲线l与曲线C的两个交点，则|AB|=（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | $\sqrt{6}$ |
19．如图所示是y=Asin（ωx+φ）（A＞0，ω＞0）的图象的一段，它的一个解析式为（ ）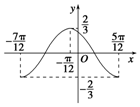 
| A． | y=$\frac{2}{3}$sin（2x+$\frac{π}{3}$） | B． | y=$\frac{2}{3}$sin（$\frac{x}{2}$+$\frac{π}{4}$） | C． | y=$\frac{2}{3}$sin（x-$\frac{π}{3}$） | D． | y=$\frac{2}{3}$sin（2x+$\frac{2}{3}$π） |
6．“a≠1或b≠2”是“a+b≠3”的（ ）
| A． | 必要不充分条件 | B． | 既不充分也不必要条件 | ||
| C． | 充要条件 | D． | 充分不必要条件 |
3．设f（x）是定义在R上的奇函数，其图象关于直线x=1对称，且当0＜x≤1时，f（x）=log3x．记f（x）在[-10，10]上零点的个数为m，方程f（x）=-1在[-10，10]上的实数根和为n，则有（ ）
| A． | m=20，n=10 | B． | m=10，n=20 | C． | m=21，n=10 | D． | m=11，n=21 |