题目内容
已知2a+b+2ab=3,a>0,b>0,则2a+b有( )
| A、最大值2 | ||
B、最大值3-
| ||
| C、最小值2 | ||
D、最小值3-
|
考点:基本不等式
专题:不等式的解法及应用
分析:由a>0,b>0,利用基本不等式的性质可得3=2a+b+2ab≤2a+b+
,再利用一元二次不等式的解法即可得出.
| (2a+b)2 |
| 4 |
解答:
解:∵a>0,b>0,∴3=2a+b+2ab≤2a+b+
,
化为(2a+b)2+4(2a+b)-12≥0,
因式分解为(2a+b+6)(2a+b-2)≥0,
解得2a+b≥2.
∴2a+b有最小值2.
故选:C.
| (2a+b)2 |
| 4 |
化为(2a+b)2+4(2a+b)-12≥0,
因式分解为(2a+b+6)(2a+b-2)≥0,
解得2a+b≥2.
∴2a+b有最小值2.
故选:C.
点评:本题考查了基本不等式的性质、一元二次不等式的解法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
下列说法中正确的是( )
| A、棱柱的侧面可以是三角形 |
| B、正方体和长方体都是特殊的四棱柱 |
| C、棱柱的各条棱都相等 |
| D、所有的几何体的表面都展成平面图形 |
下列等式不正确的是( )
①
+(
+
)=(
+
)+
②
+
≠
,
③
=
+
+
.
①
| a |
| b |
| c |
| a |
| c |
| b |
②
| AB |
| BA |
| 0 |
③
| AC |
| DC |
| AB |
| BD |
| A、②③ | B、② | C、① | D、③ |
函数y=sinx(x∈[-π,π])图象与x轴围成的图形的面积是( )
| A、0 | B、1 | C、2 | D、4 |
若函数f(x)=
在R上为增函数,则实数a的取值范围是( )
|
| A、(0,2] |
| B、(-∞,2) |
| C、(1,2] |
| D、(-∞,2] |
已知向量
、
,|
|=2,
=(3,4),
与
夹角等于60°,则
•
等于( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、5 | ||||
B、
| ||||
C、5
| ||||
D、5
|
为了对某课题进行研究,用分层抽样方法从三所科研单位A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人):则( )
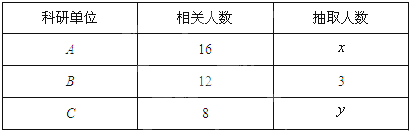

| A、x=6,y=4 |
| B、x=4,y=3 |
| C、x=7,y=4 |
| D、x=4,y=2 |