题目内容
如果函数af(x)=
-x-a有三个零点,则a的取值范围是 .
| x3 |
| 3 |
考点:利用导数研究函数的极值
专题:导数的综合应用
分析:由f(x)=
-x-a=0得
-x=a,利用导数求出函数y=f(x)=
-x的极值,利用数形结合即可得到结论.
| x3 |
| 3 |
| x3 |
| 3 |
| x3 |
| 3 |
解答:
解:由f(x)=
-x-a=0的
-x=a,
设g(x)=
-x,
则函数的g(x)的导数g′(x)=x2-1,
由g′(x)≥0,解得x≥1或x≤-1,此时函数单调递增,
由g′(x)<0,解得-1<x<1,即此时函数单调递减,
故函数的极大值f(-1)=
,极小值为f(1)=-
,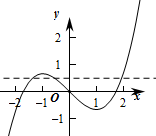
∴要使函数f(x)=
-x-a有三个零点,
则-
<a<
,
故答案为:(-
,
)
| x3 |
| 3 |
| x3 |
| 3 |
设g(x)=
| x3 |
| 3 |
则函数的g(x)的导数g′(x)=x2-1,
由g′(x)≥0,解得x≥1或x≤-1,此时函数单调递增,
由g′(x)<0,解得-1<x<1,即此时函数单调递减,
故函数的极大值f(-1)=
| 2 |
| 3 |
| 2 |
| 3 |
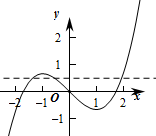
∴要使函数f(x)=
| x3 |
| 3 |
则-
| 2 |
| 3 |
| 2 |
| 3 |
故答案为:(-
| 2 |
| 3 |
| 2 |
| 3 |
点评:本题主要考查函数零点个数的应用,利用导数研究函数的极值是解决本题的关键.

练习册系列答案
相关题目
从1,2,3,4,5 这5个数字中,任取两数,其中一个数为奇数,另一个数为偶数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|