题目内容
11.如果P1,P2,…,Pn是抛物线C:y2=4x上的点,它们的横坐标依次为x1,x2,…,xn,F是抛物线C的焦点,若x1+x2+…+xn=10,则|P1F|+|P2F|+…+|PnF|=( )| A. | n+10 | B. | n+20 | C. | 2n+10 | D. | 2n+20 |
分析 由抛物线性质得|PnF|=${x}_{n}+\frac{p}{2}$=xn+1,由此能求出结果.
解答 解:∵P1,P2,…,Pn是抛物线C:y2=4x上的点,
它们的横坐标依次为x1,x2,…,xn,F是抛物线C的焦点,
x1+x2+…+xn=10,
∴|P1F|+|P2F|+…+|PnF|
=(x1+1)+(x2+1)+…+(xn+1)
=x1+x2+…+xn+n
=n+10.
故选:A.
点评 本题考查抛物线中一组线段和的求法,是中档题,解题时要认真审题,注意抛物线的性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.设函数$f(x)={e^{|x|}}-\frac{2}{{{x^2}+3}}$,则使得f(x)>f(2x-1)成立的x的取值范围是( )
| A. | $(\frac{1}{3},1)$ | B. | $(-∞,\frac{1}{3})∪(1,+∞)$ | C. | $(-\frac{1}{3},\frac{1}{3})$ | D. | $(-∞,-\frac{1}{3})∪(\frac{1}{3},+∞)$ |
20.已知抛物线y=4ax2,则其准线方程是( )
| A. | y=-$\frac{1}{16a}$ | B. | x=-a | C. | y=±$\frac{1}{16a}$ | D. | x=±a |
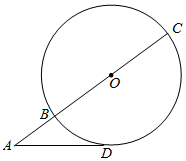 如图,BC为⊙O的直径,且BC=6,延长CB与⊙O在点D处的切线交于点A,若AD=4,则AB=2.
如图,BC为⊙O的直径,且BC=6,延长CB与⊙O在点D处的切线交于点A,若AD=4,则AB=2.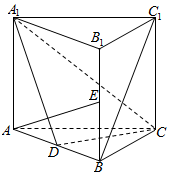 如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=$\sqrt{2}$,AA1=AC=CB=1.
如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=$\sqrt{2}$,AA1=AC=CB=1.