题目内容
19.对于函数f(x),如果存在函数g(x)=ax+b(a,b为常数),使得对于区间D上的一切实数x都有f(x)≤g(x)成立,则称函数g(x)为函数f(x)在区间D上的一个“覆盖函数”,设f(x)=2x,g(x)=2x,若函数g(x)为函数f(x)在区间[m,n]上的一个“覆盖函数”,则2|m-n|的最大值为2.分析 由2|m-n|的最大值,知需找|m-n|的最大值,由2x≤2x恒成立,知1≤x≤2,所以得|m-n|最大为1,所以2|m-n|的最大值为2.
解答 解:求解2|m-n|的最大值,即为寻找|m-n|的最大值,
∵f(x)=2x,g(x)=2x,
要想对于区间D上的一切实数x都有f(x)≤g(x)成立,
即2x≤2x恒成立,
则1≤x≤2,
∴区间[m,n]的最大跨度为2-1=1,
∴2|m-n|的最大值为2.
故答案为:2.
点评 本题考查指数函数单调性和数形结合问题.

练习册系列答案
相关题目
14.若某项试验的成功率是失败率的2倍,用离散型随机变量X描述1次试验成功的次数,则P(X=1)等于( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
11.如果P1,P2,…,Pn是抛物线C:y2=4x上的点,它们的横坐标依次为x1,x2,…,xn,F是抛物线C的焦点,若x1+x2+…+xn=10,则|P1F|+|P2F|+…+|PnF|=( )
| A. | n+10 | B. | n+20 | C. | 2n+10 | D. | 2n+20 |
9.等差数列{an}中,a1+a4+a7=48,a2+a5+a8=40,则a3+a6+a9的值是( )
| A. | 30 | B. | 32 | C. | 34 | D. | 36 |
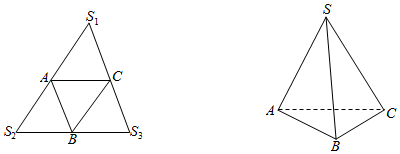
 如图,三个边长为2的等边三角形有一条边在同一条直线上,边B3C3上有10个不同的点P1,P2,…P10,记mi=$\overrightarrow{A{B}_{2}}$•$\overrightarrow{A{P}_{i}}$(i=1,2,3,…,10),则m1+m2+…+m10的值为180.
如图,三个边长为2的等边三角形有一条边在同一条直线上,边B3C3上有10个不同的点P1,P2,…P10,记mi=$\overrightarrow{A{B}_{2}}$•$\overrightarrow{A{P}_{i}}$(i=1,2,3,…,10),则m1+m2+…+m10的值为180.