题目内容
12.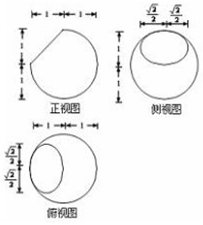 半径为1的球被一平面截去部分得一个几何体,其三视图和尺寸如图所示,则球心到该截面的距离为( )
半径为1的球被一平面截去部分得一个几何体,其三视图和尺寸如图所示,则球心到该截面的距离为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
分析 由已知三视图可得,截面的直径为$\sqrt{2}$,进而可得球心到该截面的距离.
解答 解:由已知三视图可得,截面的直径为$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
故截面半径r=$\frac{\sqrt{2}}{2}$,
又由球半径R=1,
故球心到该截面的距离d=$\sqrt{{R}^{2}-{r}^{2}}$=$\frac{\sqrt{2}}{2}$,
故选:C
点评 本题考查的知识点是球的几何特征,简单几何体的三视图,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.若向量$\overrightarrow{a}$(-1,1),$\overrightarrow{b}$(3,-2),则|$\overrightarrow{a}$-$\overrightarrow{b}$|=( )
| A. | $\sqrt{6}$ | B. | 5 | C. | $\sqrt{5}$ | D. | 6 |
4. 如图是一个四面体的三视图,图中三个三角形均为直角三角形,且面积之和为8,则其外接球的表面积的最小值为( )
如图是一个四面体的三视图,图中三个三角形均为直角三角形,且面积之和为8,则其外接球的表面积的最小值为( )
 如图是一个四面体的三视图,图中三个三角形均为直角三角形,且面积之和为8,则其外接球的表面积的最小值为( )
如图是一个四面体的三视图,图中三个三角形均为直角三角形,且面积之和为8,则其外接球的表面积的最小值为( )| A. | 16π | B. | 8π | C. | $\frac{32π}{3}$ | D. | $\frac{16π}{3}$ |
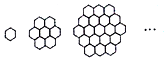 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似的看作是一个正六边形,如图为一组蜂巢的截面图,其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,第六幅图的蜂巢总数为91.
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似的看作是一个正六边形,如图为一组蜂巢的截面图,其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,第六幅图的蜂巢总数为91.