题目内容
2.已知函数f(x)=2$\sqrt{3}$sin(π-x)cosx+2cos2x+a-1.(Ⅰ)求f(x)的最小正周期;
(Ⅱ)若f(x)在区间[-$\frac{π}{6}$,$\frac{π}{3}$]上的最大值与最小值的和为2,求a的值.
分析 (I)利用倍角公式与和差公式可得:函数f(x)=2$sin(2x+\frac{π}{6})$+a.可得f(x)的最小正周期T.
(II)由x∈[-$\frac{π}{6}$,$\frac{π}{3}$],可得$-\frac{π}{6}$≤2x+$\frac{π}{6}$≤$\frac{5π}{6}$,可得$sin(2x+\frac{π}{6})$∈$[-\frac{1}{2},1]$.进而得出答案.
解答 解:(I)函数f(x)=2$\sqrt{3}$sin(π-x)cosx+2cos2x+a-1=$\sqrt{3}$sin2x+cos2x+a
=2$sin(2x+\frac{π}{6})$+a.
∴f(x)的最小正周期T=$\frac{2π}{2}$=π.
(II)∵x∈[-$\frac{π}{6}$,$\frac{π}{3}$],∴$-\frac{π}{6}$≤2x+$\frac{π}{6}$≤$\frac{5π}{6}$,∴$sin(2x+\frac{π}{6})$∈$[-\frac{1}{2},1]$.
∴f(x)∈[a-1,a+2].
∴a-1+a+2=2,解得a=$\frac{1}{2}$.
点评 本题考查了倍角公式与和差公式、三角函数的图象与性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12.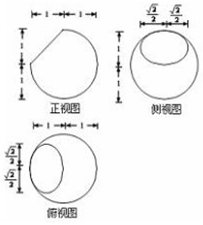 半径为1的球被一平面截去部分得一个几何体,其三视图和尺寸如图所示,则球心到该截面的距离为( )
半径为1的球被一平面截去部分得一个几何体,其三视图和尺寸如图所示,则球心到该截面的距离为( )
 半径为1的球被一平面截去部分得一个几何体,其三视图和尺寸如图所示,则球心到该截面的距离为( )
半径为1的球被一平面截去部分得一个几何体,其三视图和尺寸如图所示,则球心到该截面的距离为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
13.若a,b∈R,直线l:y=ax+b,圆C:x2+y2=1.命题p:直线l与圆C相交;命题q:a>$\sqrt{{b^2}-1}$.则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为$\sqrt{5}$,圆心在x轴的正半轴上的圆M与双曲线的渐近线相切,且圆M的半径为2,则以圆M的圆心为焦点的抛物线的标准方程为( )
| A. | y2=8$\sqrt{5}$x | B. | y2=4$\sqrt{5}$x | C. | y2=2$\sqrt{5}$x | D. | y2=$\sqrt{5}$x |
7.在(3x2-$\frac{1}{x}$)6的二项展开式中,x3项的系数为( )
| A. | 540 | B. | -540 | C. | 20 | D. | -20 |
 设函数y=f(x)在区间[0,1]上的图象是连续不断的一条曲线,且恒有0≤f(x)≤1,可以用随机模拟方法近似计算由曲线y=f(x)及直线x=0,x=1,y=0所围成部分的面积S,先生产两组(每组N个)区间[0,1]上均匀随机数x1,x2,…,xN和y1,y2,…,yN,由此得到N个点(xi,yi)(i=1,2,…,N),再数出其中满足yi≤f(xi)(i=1,2,…,N)的点数N1,那么由随机模拟方法可得S的近似值为$\frac{{N}_{1}}{N}$.
设函数y=f(x)在区间[0,1]上的图象是连续不断的一条曲线,且恒有0≤f(x)≤1,可以用随机模拟方法近似计算由曲线y=f(x)及直线x=0,x=1,y=0所围成部分的面积S,先生产两组(每组N个)区间[0,1]上均匀随机数x1,x2,…,xN和y1,y2,…,yN,由此得到N个点(xi,yi)(i=1,2,…,N),再数出其中满足yi≤f(xi)(i=1,2,…,N)的点数N1,那么由随机模拟方法可得S的近似值为$\frac{{N}_{1}}{N}$. PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.