题目内容
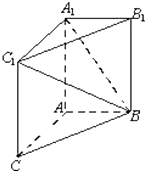 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,AB⊥平面AA1C1C,AB=3.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,AB⊥平面AA1C1C,AB=3.(Ⅰ)求直线A C1与直线A1B夹角的余弦值;
(Ⅱ)求二面角A1-BC1-B1的余弦值.
考点:用空间向量求平面间的夹角,异面直线及其所成的角
专题:计算题,空间位置关系与距离,空间角
分析:(I)由线面垂直的性质和判定,即可得到AA1⊥平面ABC,AB⊥AC,以A为坐标原点,AC,AB,AA1所在直线为x,y,z轴,建立空间直角坐标系,求出A1(0,0,4),B(0,3,0),C1(4,0,4),则
=(4,0,4),
=(0,3,-4),再由向量的夹角公式即可得到所求值;
(II)通过(Ⅰ)建立的空间直角坐标系,设出所求的两个平面的法向量,运用向量垂直的条件:数量积为0,再利用两个平面的法向量的夹角即可得到二面角.
| AC1 |
| A1B |
(II)通过(Ⅰ)建立的空间直角坐标系,设出所求的两个平面的法向量,运用向量垂直的条件:数量积为0,再利用两个平面的法向量的夹角即可得到二面角.
解答:
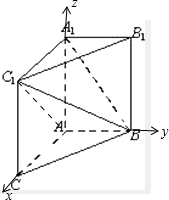 解:(I)∵AA1C1C是正方形,∴AA1⊥AC
解:(I)∵AA1C1C是正方形,∴AA1⊥AC
又∵AB⊥平面AA1C1C,AB⊥AC,AB⊥AA1,
∴AA1⊥平面ABC,由AC=4,AB=3,得BC=5,
以A为坐标原点,AC,AB,AA1所在直线为x,y,z轴,
建立如图所示的空间直角坐标系,则A1(0,0,4),B(0,3,0),
C1(4,0,4),则
=(4,0,4),
=(0,3,-4),
cos<
,
>=
=
=-
.
故直线A C1与直线A1B夹角的余弦值为
;
(Ⅱ)由(Ⅰ)得A1(0,0,4),B(0,3,0),B1(0,3,4),
C1(4,0,4),∴
=(0,-3,4),
=(4,-3,4),
=(0,0,4),
设平面A1BC1的法向量为
=(x1,y1,z1),
平面B1BC1的法向量为
=(x2,y2,z2).
则
,
令y1=4,解得x1=0,z1=3,∴
=(0,4,3),
,
令x2=3,解得y2=4,z2=0,∴
=(3,4,0).
cos<
,
>=
=
=
.
∴二面角A1-BC1-B1的余弦值为
.
 解:(I)∵AA1C1C是正方形,∴AA1⊥AC
解:(I)∵AA1C1C是正方形,∴AA1⊥AC又∵AB⊥平面AA1C1C,AB⊥AC,AB⊥AA1,
∴AA1⊥平面ABC,由AC=4,AB=3,得BC=5,
以A为坐标原点,AC,AB,AA1所在直线为x,y,z轴,
建立如图所示的空间直角坐标系,则A1(0,0,4),B(0,3,0),
C1(4,0,4),则
| AC1 |
| A1B |
cos<
| AC1 |
| A1B |
| ||||
|
|
| -16 | ||
4
|
2
| ||
| 5 |
故直线A C1与直线A1B夹角的余弦值为
2
| ||
| 5 |
(Ⅱ)由(Ⅰ)得A1(0,0,4),B(0,3,0),B1(0,3,4),
C1(4,0,4),∴
| BA1 |
| BC1 |
| BB1 |
设平面A1BC1的法向量为
| n1 |
平面B1BC1的法向量为
| n2 |
则
|
令y1=4,解得x1=0,z1=3,∴
| n1 |
|
令x2=3,解得y2=4,z2=0,∴
| n2 |
cos<
| n1 |
| n2 |
| ||||
|
|
| 16 | ||||
|
| 16 |
| 25 |
∴二面角A1-BC1-B1的余弦值为
| 16 |
| 25 |
点评:本题综合考查了线面垂直的判定与性质定理、面面垂直的性质定理、通过建立空间直角坐标系利用法向量求二面角的方法、向量垂直与数量积得关系等基础知识与基本方法,考查了空间想象能力、推理能力和计算能力.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
下列四个关系式中,正确的是( )
| A、1∈{1,2} |
| B、1⊆{1,2} |
| C、{1}∈{1,2} |
| D、{1}={1,2} |
若某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )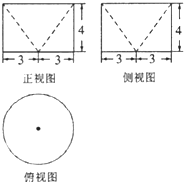

| A、33πcm2 |
| B、42πcm2 |
| C、48πcm2 |
| D、52πcm2 |
已知双曲线
-
=1(a>0,b>0)的左右焦点分别为F1,F2,过F1的直线分别交双曲线的两条渐近线于点P,Q.若点P是线段F1Q的中点,且QF1⊥QF2,则此双曲线的离心率等于( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、2 | ||
C、
| ||
D、
|
直线y=kx+3与圆(x-3)2+(y-2)2=4相交于M,N两点,若|MN|≥2
,则k的取值范围是( )
| 3 |
A、[-
| ||||||||
B、[-∞,-
| ||||||||
C、[-
| ||||||||
D、[-
|