题目内容
8．已知几何体的三视图如图所示，则该几何体的表面积是（ ）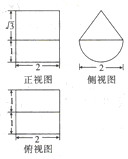
| A． | $2π+16+2\sqrt{3}$ | B． | $3π+16+2\sqrt{3}$ | C． | $3π+8+\sqrt{3}$ | D． | $3π+8+2\sqrt{3}$ |
分析 由三视图可知该几何体是一个半圆柱和一个三棱柱的组合体．
解答 解：由三视图可知该几何体是一个半圆柱和一个三棱柱的组合体，
故其表面积为$π×1×2+π+{2^2}×2+2×\frac{1}{2}×2×\sqrt{3}=3π+8+2\sqrt{3}$，
故选：D．
点评 本题考查了圆柱和三棱柱的三视图及其表面积计算公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
18．
一个四面体的三视图如右图，在三视图中的三个正方形的边长都是$\sqrt{2}$，则该多面体的体积、表面积、外接球面的表面积分别为（ ）
一个四面体的三视图如右图，在三视图中的三个正方形的边长都是$\sqrt{2}$，则该多面体的体积、表面积、外接球面的表面积分别为（ ）| A． | 2$\sqrt{2}$，12，4π | B． | $\frac{2\sqrt{2}}{3}$，4$\sqrt{3}$，6π | C． | $\frac{\sqrt{3}}{3}$，6，$\sqrt{6}$π | D． | $\sqrt{2}$，2$\sqrt{3}$，$\frac{2}{3}$π |
20．
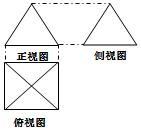如果一个几何体的三视图如图所示，正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形，（单位长度：cm），则此几何体的侧面积是（ ）
如果一个几何体的三视图如图所示，正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形，（单位长度：cm），则此几何体的侧面积是（ ）| A． | .$2\sqrt{3}$cm | B． | .$4\sqrt{3}$cm2 | C． | 8 cm2 | D． | 12 cm2 |
17．某电脑公司有6名产品推销员，其工作年限与年推销金额的数据如表：
（1）以工作年限为自变量，推销金额为因变量y，作出散点图；
（2）求年推销金额y关于工作年限x的线性回归方程；
（3）若第6名推销员的工作年限为11年，试估计他的年推销金额．
附：回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中，$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{5}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{5}（{x}_{i}-\overline{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$．
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x/年 | 3 | 5 | 6 | 7 | 9 |
| 推销金额y/万元 | 2 | 3 | 3 | 4 | 5 |
（2）求年推销金额y关于工作年限x的线性回归方程；
（3）若第6名推销员的工作年限为11年，试估计他的年推销金额．
附：回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中，$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{5}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{5}（{x}_{i}-\overline{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$．
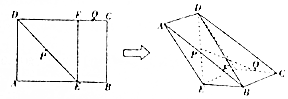已知矩形ABCD中，E、F分别是AB、CD上的点，BE=CF=1，BC=2，AB=CD=3，P、Q分别为DE、CF的中点，现沿着EF翻折，使得二面角A-EF-B大小为$\frac{2π}{3}$．