题目内容
11.设a=($\frac{1}{3}$)${\;}^{\frac{4}{5}}$,b=($\frac{1}{4}$)${\;}^{\frac{4}{5}}$,c=($\frac{1}{3}$)${\;}^{\frac{3}{5}}$,则( )| A. | a<b<c | B. | c<a<b | C. | b<c<a | D. | b<a<c |
分析 利用幂函数y=x${\;}^{\frac{4}{5}}$,单调递增,指数函数y=($\frac{1}{3}$)x,单调递减,即可得出结论.
解答 解:考查幂函数y=x${\;}^{\frac{4}{5}}$,单调递增,∵$\frac{1}{3}>\frac{1}{4}$,∴a>b,
考查指数函数y=($\frac{1}{3}$)x,单调递减,∵$\frac{4}{5}>\frac{3}{5}$,∴c>a,
故选D.
点评 本题考查幂函数、指数函数的单调性,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
2.已知等边△ABC的边长为2$\sqrt{3}$,动点P、M满足|$\overrightarrow{AP}$|=1,$\overrightarrow{PM}$=$\overrightarrow{MC}$,则|$\overrightarrow{BM}$|2的最小值是( )
| A. | $\frac{25}{4}$ | B. | $\frac{31}{4}$ | C. | $\frac{37-6\sqrt{3}}{4}$ | D. | $\frac{37-2\sqrt{33}}{4}$ |
20.下列四组函数中,表示相等函数的一组是( )
| A. | f(x)=1,g(x)=x0 | B. | f(x)=|x|,g(t)=$\sqrt{{t}^{2}}$ | ||
| C. | f(x)=$\frac{{x}^{2}-1}{x-1}$,g(x)=x+1 | D. | f(x)=lg(x+1)+lg(x-1),g(x)=lg(x2-1) |
15.已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1、F2,短轴的一个端点为P,直线l:x+2y=0与椭圆E的一个交点为A,若|AF1|+|AF2|=10,点P到直线l的距离不大于$\frac{2\sqrt{5}}{5}$,则椭圆E的离心率的取值范围是( )
| A. | (0,$\frac{2\sqrt{6}}{5}$] | B. | [$\frac{\sqrt{3}}{2}$,1) | C. | [$\frac{2\sqrt{6}}{5}$,1) | D. | (0,$\frac{\sqrt{3}}{2}$] |
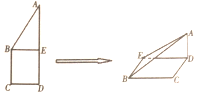 如图所示,正方形BCDE的边长为a,已知$AB=\sqrt{3}BC$,将△ABE沿BE边折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述:
如图所示,正方形BCDE的边长为a,已知$AB=\sqrt{3}BC$,将△ABE沿BE边折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述: