Question

设变量x，y满足

x-y-1≤0 x-3y+1≥0 2x-y+2≥0

，则

y-2

x+1

的取值范围是（　　）

• A、（-∞，-

  1

  3

  ]∪[3，+∞）
• B、[-3，

  1

  3

  ]
• C、[-

  1

  3

  ，3]
• D、（-∞，-3]∪[

  1

  3

  ，+∞）

Answer 1

考点：简单线性规划

专题：不等式的解法及应用

分析：作出不等式组对应的平面区域，利用目标函数的几何意义即可得到结论．

解答： 解：设k=

y-2

x+1

，则k的几何意义为区域内点到点D（-1，2）的斜率，
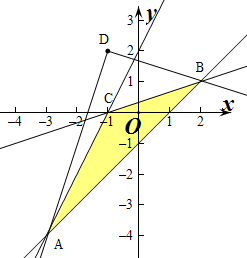
作出不等式组对应的平面区域如图：
由图象可知，
由

x-y-1=0 x-3y+1=0

解得

x=2 y=1

，即B（2，1），
由

x-y-1=0 2x-y+2=0

，解得

x=-3 y=-4

，即A（-3，-4）
则AD的斜率k=

-4-2

-3+1

=

-6

-2

=3，DB的斜率k=

1-2

2+1

=-

1

3

，
则k≤

1

3

或k≥3，
即则

y-2

x+1

的取值范围是（-∞，-

1

3

]∪[3，+∞）．
故选：A

点评：本题主要考查了用平面区域二元一次不等式组，以及简单的转化思想和数形结合的思想，属中档题．利用数形结合是解决本题的关键．