题目内容
19.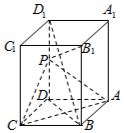 如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.(Ⅰ)求证:平面PAC⊥平面 BDD1;
(Ⅱ)求证:PB1⊥平面PAC;
(Ⅲ)求VC-PAB.
分析 (I)由长方体的结构特征可知AC⊥DD1,由底面正方形可得AC⊥BD,故AC⊥平面BDD1,从而得出平面PAC⊥平面BDD1.
(II)使用勾股定理求出PB1,PC,PA,B1C,B1A的长,利用勾股定理的逆定理得出PB1⊥PA,PB1⊥PC,故PB1⊥平面PAC;
(III)以△ABC为棱锥的底面,则PD为棱锥的高,代入体积公式计算即可.
解答 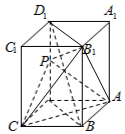 证明:(I)∵DD1⊥平面ABCD,AC?平面ABCD,
证明:(I)∵DD1⊥平面ABCD,AC?平面ABCD,
∴AC⊥DD1,
∵AB=AD,∴四边形ABCD是正方形,
∴AC⊥BD,
又BD?平面BDD1,DD1?平面BDD1,BD∩DD1=D,
∴AC⊥平面BDD1,
∵AC?平面PAC,
∴平面PAC⊥平面BDD1.
(II)连结B1C,B1A,B1D1,
∵长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,
∴B1D1=$\sqrt{2}$,PD1=PD=1,
∴PB1=$\sqrt{P{{D}_{1}}^{2}+{B}_{1}{{D}_{1}}^{2}}$=$\sqrt{3}$,PC=$\sqrt{P{D}^{2}+C{D}^{2}}$=$\sqrt{2}$,PA=$\sqrt{P{D}^{2}+A{D}^{2}}$=$\sqrt{2}$,
B1C=$\sqrt{B{C}^{2}+B{{B}_{1}}^{2}}$=$\sqrt{5}$,B1A=$\sqrt{B{{B}_{1}}^{2}+B{A}^{2}}$=$\sqrt{5}$.
∴PC2+PB12=B1C2,PA2+PB12=B1A2,
∴PB1⊥PC,PB1⊥PA,
又PA?平面PAC,PC?平面PAC,PA∩PC=P,
∴PB1⊥平面PAC.
(III)VC-PAB=VP-ABC=$\frac{1}{3}{S}_{△ABC}•PD$=$\frac{1}{3}×\frac{1}{2}×{1}^{2}×1$=$\frac{1}{6}$.
点评 本题考查了线面垂直,面面垂直的判定,棱锥的体积计算,属于中档题.

| A. | (-∞,1) | B. | (1,+∞) | C. | (-∞,1] | D. | [1,+∞) |
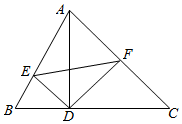 在△ABC中,AB=4,AC=6,∠BAC=60°.点A在边BC上的投影为点D.
在△ABC中,AB=4,AC=6,∠BAC=60°.点A在边BC上的投影为点D.
 如图,梯形ABCD中,AB∥CD,BC=6,tan∠ABC=-2$\sqrt{2}$.
如图,梯形ABCD中,AB∥CD,BC=6,tan∠ABC=-2$\sqrt{2}$.