题目内容
14.已知数列{an}的前n项和是Sn,且Sn+$\frac{1}{2}$an=1.(1)求数列{an}的通项公式;
(2)记bn=log${\;}_{\frac{1}{3}}$$\frac{{a}_{n}}{2}$,求数列{$\frac{1}{{b}_{n}{b}_{n+2}}$}的前n项和Tn.
分析 (1)分类讨论n=1与n≥2,从而求得数列{an}是以$\frac{2}{3}$为首项,$\frac{1}{3}$为公比的等比数列,从而解得;
(2)化简bn=log${\;}_{\frac{1}{3}}$$\frac{{a}_{n}}{2}$=n,从而利用裂项化简$\frac{1}{{b}_{n}{b}_{n+2}}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),从而求前n项和.
解答 解:(1)当n=1时,S1+$\frac{1}{2}$a1=1,
解得,a1=$\frac{2}{3}$;
当n≥2时,由Sn+$\frac{1}{2}$an=1,Sn-1+$\frac{1}{2}$an-1=1,
两式作差得:an=$\frac{1}{3}$an-1,
故数列{an}是以$\frac{2}{3}$为首项,$\frac{1}{3}$为公比的等比数列,
其通项公式为an=$\frac{2}{3}$×$\frac{1}{{3}^{n-1}}$=$\frac{2}{{3}^{n}}$;
(2)∵bn=log${\;}_{\frac{1}{3}}$$\frac{{a}_{n}}{2}$=n,
∴$\frac{1}{{b}_{n}{b}_{n+2}}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),
故Tn=$\frac{1}{2}$[(1-$\frac{1}{3}$)+($\frac{1}{2}$-$\frac{1}{4}$)+($\frac{1}{3}$-$\frac{1}{5}$)+…+($\frac{1}{n-1}$-$\frac{1}{1+n}$)+($\frac{1}{n}$-$\frac{1}{n+2}$)]
=$\frac{1}{2}$(1+$\frac{1}{2}$-$\frac{1}{1+n}$-$\frac{1}{n+2}$)
=$\frac{3}{4}$-$\frac{2n+3}{2(n+1)(n+2)}$.
点评 本题考查了数列的通项公式的求法及对数运算的应用,同时考查了裂项求和法的应用.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案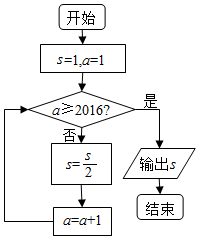
| A. | $\frac{1}{{2}^{2014}}$ | B. | $\frac{1}{{2}^{2015}}$ | C. | $\frac{1}{{2}^{2016}}$ | D. | $\frac{1}{{2}^{2017}}$ |
| A. | {x|x>1} | B. | {x|x≥1} | C. | {x|1<x≤2} | D. | {x|1≤x≤2} |

| A. | -1 | B. | 4 | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
 在三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,M为CC1的中点,∠ABC=90°,AC=A1A,∠A1AC=60°,AB=BC=2.
在三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,M为CC1的中点,∠ABC=90°,AC=A1A,∠A1AC=60°,AB=BC=2.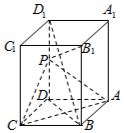 如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.