题目内容
9.已知全集U=R,P=(0,1],Q={x|2x≤1},则P∪Q=( )| A. | (-∞,1) | B. | (1,+∞) | C. | (-∞,1] | D. | [1,+∞) |
分析 解对数不等式求得Q,再根据两个集合的并集的定义求得P∪Q.
解答 解:全集U=R,P=(0,1],Q={x|2x≤1}=(-∞,0],
则P∪Q=(-∞,1],
故选:C.
点评 本题主要考查指数不等式,两个集合的并集的定义和求法,属于基础题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
20.如图是一个程序框图,则输出S的值是( )


| A. | 84 | B. | 35 | C. | 26 | D. | 10 |
17.执行如图所示的程序框图,则输出的s=( )
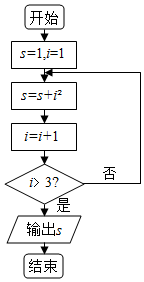

| A. | 6 | B. | 15 | C. | 25 | D. | 3 |
4.执行如图所示的程序框图,那么输出的S的值为( )


| A. | -1 | B. | 4 | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
1.复数z=$\frac{3+5i}{1+i}$(i为虚数单位)在复平面内对应点的坐标是( )
| A. | (1,4) | B. | (4,-1) | C. | (4,1) | D. | (-1,4) |
19. 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示,把f(x)的图象上各点向左平移$\frac{1}{2}$单位,得到函数g(x)的图象,则g($\frac{5}{2}$)=( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示,把f(x)的图象上各点向左平移$\frac{1}{2}$单位,得到函数g(x)的图象,则g($\frac{5}{2}$)=( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示,把f(x)的图象上各点向左平移$\frac{1}{2}$单位,得到函数g(x)的图象,则g($\frac{5}{2}$)=( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示,把f(x)的图象上各点向左平移$\frac{1}{2}$单位,得到函数g(x)的图象,则g($\frac{5}{2}$)=( )| A. | -1 | B. | 1 | C. | -$\sqrt{3}$ | D. | $\sqrt{3}$ |
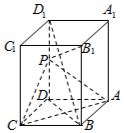 如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.