题目内容
8. 如图,梯形ABCD中,AB∥CD,BC=6,tan∠ABC=-2$\sqrt{2}$.
如图,梯形ABCD中,AB∥CD,BC=6,tan∠ABC=-2$\sqrt{2}$.(Ⅰ)若∠ACD=$\frac{π}{4}$,求AC的长;
(Ⅱ)若BD=9,求△BCD的面积.
分析 (Ⅰ)由已知和同角三角函数基本关系可得sin∠ABC,sin∠CAB,由正弦定理可得AC=$\frac{BCsin∠ABC}{sin∠CAB}$,代值计算可得;
(Ⅱ)由题意可得sin∠BCD和cos∠BCD,由正弦定理可得sin∠BDC,进而可得cos∠BDC,由和差角的三角函数公式可得sin∠CBD=sin(∠BCD+∠BDC)=sin∠BCDcos∠BDC+cos∠BCDsin∠BDC,代入计算可得其值,代入S=$\frac{1}{2}$BC•BD•sin∠CBD,计算可得.
解答 解:(Ⅰ)∵梯形ABCD中,AB∥CD,BC=6,tan∠ABC=-2$\sqrt{2}$,
∴由同角三角函数基本关系可得sin∠ABC=$\frac{2\sqrt{2}}{3}$,
又∵∠ACD=$\frac{π}{4}$,∴由内错角相等可得∠CAB=∠ACD=$\frac{π}{4}$,
在△ABC中由正弦定理可得AC=$\frac{BCsin∠ABC}{sin∠CAB}$=$\frac{6×\frac{2\sqrt{2}}{3}}{\frac{\sqrt{2}}{2}}$=8;
(Ⅱ)由(Ⅰ)可得sin∠ABC=$\frac{2\sqrt{2}}{3}$,
∴sin∠BCD=sin(π-∠ABC)=sin∠ABC=$\frac{2\sqrt{2}}{3}$,
∴cos∠BCD=$\sqrt{1-si{n}^{2}∠BCD}$=$\frac{1}{3}$,
∴在△BCD中由正弦定理可得:
sin∠BDC=$\frac{BC•sin∠BCD}{BD}$=$\frac{6×\frac{2\sqrt{2}}{3}}{9}$=$\frac{4\sqrt{2}}{9}$,
∴cos∠BDC=$\sqrt{1-si{n}^{2}∠BDC}$=$\frac{7}{9}$,
∴sin∠CBD=sin(∠BCD+∠BDC)
=sin∠BCDcos∠BDC+cos∠BCDsin∠BDC
=$\frac{2\sqrt{2}}{3}×\frac{7}{9}$+$\frac{1}{3}×\frac{4\sqrt{2}}{9}$=$\frac{2\sqrt{2}}{3}$
∴△BCD的面积S=$\frac{1}{2}$BC•BD•sin∠CBD=$\frac{1}{2}×6×9×\frac{2\sqrt{2}}{3}$=18$\sqrt{2}$.
点评 本题考查解三角形,涉及正余弦定理和三角函数公式,数形结合是解决问题的关键,属中档题.

| A. | {x|x>1} | B. | {x|x≥1} | C. | {x|1<x≤2} | D. | {x|1≤x≤2} |
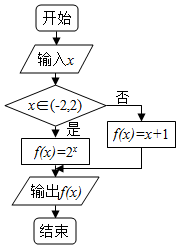
| A. | [0,2) | B. | [2,7] | C. | [2,4] | D. | [0,7] |

| A. | 84 | B. | 35 | C. | 26 | D. | 10 |
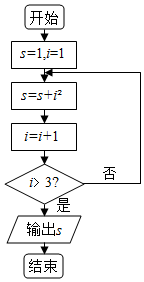
| A. | 6 | B. | 15 | C. | 25 | D. | 3 |
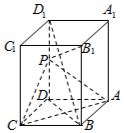 如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.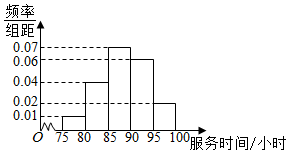 某市教育部门规定,高中学生三年在校期间必须参加不少于80小时的社区服务,教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.
某市教育部门规定,高中学生三年在校期间必须参加不少于80小时的社区服务,教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.