题目内容
已知曲线y=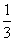 x3+
x3+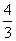 .
.
(1)求曲线在点P(2,4)处的切线方程;
(2)求曲线过点P(2,4)的切线方程.
y=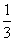 x3+
x3+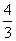 ,则y′=x2.
,则y′=x2.
(1)由题意可知点P(2,4)为切点,
y′|x=2=22=4,
所以曲线在点P(2,4)处的切线方程为y-4=4(x-2),即4x-y-4=0.
(2)由题意可知点P(2,4)不一定为切点,故设切点为(x0,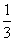 x
x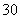 +
+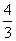 ),
),
y′|x=x0=x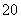 ,
,
曲线过点P(2,4)的切线方程为y-(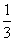 x
x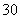 +
+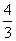 )=x
)=x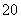 (x-x0),
(x-x0),
所以4-(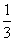 x
x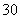 +
+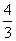 )=x
)=x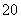 (2-x0),
(2-x0),
x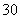 -3x
-3x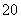 +4=0⇔(x
+4=0⇔(x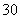 +1)-3(x
+1)-3(x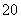 -1)=0⇔(x0+1)(x
-1)=0⇔(x0+1)(x -4x0+4)=0.
-4x0+4)=0.
解得x0=-1或x0=2,
即切点为(-1,1)或(2,4).
所以曲线过点P(2,4)的切线方程为x-y+2=0或4x-y-4=0.

练习册系列答案
相关题目
 7 19
7 19
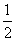 bx2+cx+d(a,b,c>0)上存在斜率为0的切线,则
bx2+cx+d(a,b,c>0)上存在斜率为0的切线,则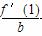 -1的取值范围是( )
-1的取值范围是( )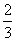 ,2);
,2);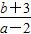 的取值范围是( )
的取值范围是( )
 )∪(3,+∞)
)∪(3,+∞) ,3)
,3)