题目内容
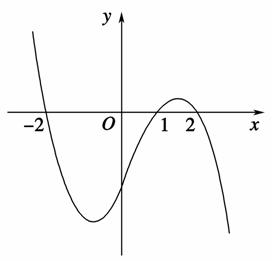
设函数f(x)在R上可导,其导函数为f ′(x),且函数y=(1-x)f ′(x)的图象如下图所示,则下列结论中一定成立的是( )
A.函数f(x)有极大值f(2)和极小值f(1)
B.函数f(x)有极大值f(-2)和极小值f(1)
C.函数f(x)有极大值f(2)和极小值f(-2)
D.函数f(x)有极大值f(-2)和极小值f(2)
D
[解析] 当x<-2时,1-x>3,则f ′(x)>0;
当-2<x<1时,0<1-x<3,则f ′(x)<0;
∴函数f(x)有极大值f(-2),当1<x<2时,-1<1-x<0,则f ′(x)<0;x>2时,1-x<-1,则f ′(x)>0,
∴函数f(x)有极小值f(2),故选D.

练习册系列答案
相关题目
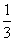 ax3+
ax3+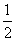 bx2+cx+d(a,b,c>0)上存在斜率为0的切线,则
bx2+cx+d(a,b,c>0)上存在斜率为0的切线,则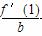 -1的取值范围是( )
-1的取值范围是( ) B.0
B.0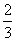 ,2);
,2); B.f(x1)<0,f(x2)<-
B.f(x1)<0,f(x2)<-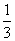 x3+81x-234,则使该生产厂家获取最大年利润的年产量为( )
x3+81x-234,则使该生产厂家获取最大年利润的年产量为( ) (1-t)3dt,则f(x)的展开式中x的系数是( )
(1-t)3dt,则f(x)的展开式中x的系数是( )