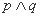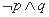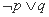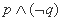题目内容
“φ=π”是“曲线y=sin(2x+φ)过坐标原点”的________条件.
充分而不必要
解析 当φ=π时,y=sin(2x+π)=-sin 2x,
则曲线y=-sin 2x过坐标原点,
所以“φ=π”⇒“曲线y=sin(2x+φ)过坐标原点”;
当φ=2π时,y=sin(2x+2π)=sin 2x,
则曲线y=sin 2x过坐标原点,
所以“φ=π” 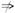 “曲线y=sin(2x+φ)过坐标原点”,
“曲线y=sin(2x+φ)过坐标原点”,
所以“φ=π”是“曲线y=sin(2x+φ)过坐标原点”的充分而不必要条件.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
命题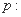
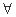
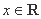 ,
,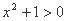 ,命题
,命题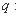
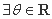 ,
,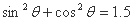 ,则下列命题中真命题是( )
,则下列命题中真命题是( )
| (A) | (B) | (C) | (D) |
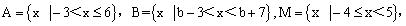 全集U=R.
全集U=R.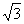 ,焦点坐标为
,焦点坐标为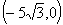 和
和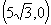 的双曲线
的双曲线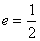 ,准线方程为
,准线方程为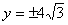 的椭圆
的椭圆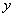 轴,焦点到准线的距离为4的抛物线
轴,焦点到准线的距离为4的抛物线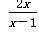 <1,q:(x-a)(x-3)>0,若綈p是綈q的必要不充分条件,则实数a的取值范围是________.
<1,q:(x-a)(x-3)>0,若綈p是綈q的必要不充分条件,则实数a的取值范围是________.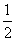 },则f(10x)>0的解集为________.
},则f(10x)>0的解集为________.