题目内容
已知A（4，0），B（-3，
）是椭圆
+
=1内的点，M是椭圆上的动点，则|MA|+|MB|的最大值是 ．
| 3 |
| x2 |
| 25 |
| y2 |
| 9 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：由椭圆
+
=1可得A（4，0）是椭圆的右焦点，设A′（-4，0）为椭圆的左焦点．由定义可得|MA|+|MA′|=2a=10，利用三角形的三边共线可得|MA|+|MB|=10-|MA′|+|MB|≤10+|A′B|，即可得出．
| x2 |
| 25 |
| y2 |
| 9 |
解答：
解：由椭圆
+
=1可得a=5，b=3，c=4，因此A（4，0）是椭圆的右焦点，设A′（-4，0）为椭圆的左焦点．
则|MA|+|MA′|=2a=10，
∴|MA|+|MB|=10-|MA′|+|MB|≤10+|A′B|=10+
=12，当且仅当三点M，A′，B共线时取等号．
∴|MA|+|MB|的最大值是12．
故答案为：12．
| x2 |
| 25 |
| y2 |
| 9 |
则|MA|+|MA′|=2a=10，
∴|MA|+|MB|=10-|MA′|+|MB|≤10+|A′B|=10+
12+(
|
∴|MA|+|MB|的最大值是12．
故答案为：12．
点评：本题考查了椭圆的定义、三角形三边的大小关系，考查了推理能力与计算能力，属于中档题．
练习册系列答案
优生乐园系列答案
相关题目
设函数y=
的反函数为f-1（x），函数g（x）与f（x+1）的图象关于直线y=x对称，那么g（2）的值为（ ）
| 1-x |
| 1+x |
| A、-2 | ||
| B、-1 | ||
C、-
| ||
D、-
|
设a，b，c表示三条不同直线，α，β表示两个不同平面，则下列命题中逆命题不成立的是（ ）
| A、b?β，c是α在β内的射影，若b⊥c，则b⊥a |
| B、b?α，c?α，若c∥α，则b∥c |
| C、c⊥α，若c⊥β，则α∥β |
| D、b?β，若b⊥α，则β⊥α |
如图所示，在边长为2的正方形中有一封闭曲线围成的阴影区域．在正方形中随机撒一粒豆子，它落在阴影区域内的概率为若椭圆两准线间的距离等于焦距的4倍，则此椭圆的离心率为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如果一个几何体的三视图如图所示（单位长度：cm），则此几何体的表面积是（ ）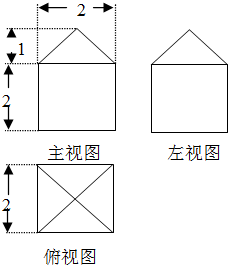
A、（20+4
| ||
| B、21 cm | ||
C、（24+4
| ||
| D、24 cm |