题目内容
有大小形状相同的3个红色小球和5个白色小球,排成一排,共有 种不同的排列方法.
考点:排列、组合及简单计数问题
专题:计算题,排列组合
分析:8个小球排好后对应着8个位置,题中的排法相当于在8个位置中选出3个位置给红球,剩下的位置给白球,由于这3个红球完全相同,所以没有顺序,是组合问题.
解答:
解:8个小球排好后对应着8个位置,题中的排法相当于在8个位置中选出3个位置给红球,剩下的位置给白球,由于这3个红球完全相同,所以没有顺序,是组合问题.这样共有:
=56排法.
故答案为:56.
| C | 3 8 |
故答案为:56.
点评:本题考查排列、组合及简单计数问题,考查学生的计算能力,确定题中的排法相当于在8个位置中选出3个位置给红球,剩下的位置给白球是关键.

练习册系列答案
相关题目
某舞台灯光设计师为了在地板上设计图案,他把一端向下发光的光源和支架之间的角度固定为θ角,支架的一端固定在地板的中心位置,支架的另一端固定在天花板的适当位置,当光源围绕支架以θ角快速旋转时,地板上可能出现的图案有( )
| A、椭圆 | B、抛物线 |
| C、圆 | D、以上均有可能 |
正四面体的内切球与外接球的半径的比等于( )
| A、1:3 | B、1:2 |
| C、2:3 | D、3:5 |
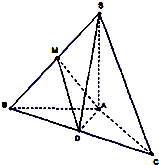 如图,在三棱锥S-ABC中,SA⊥平面ABC,AB=AC=1,SA=2,D为BC的中点.M为SB上的点,且AM=
如图,在三棱锥S-ABC中,SA⊥平面ABC,AB=AC=1,SA=2,D为BC的中点.M为SB上的点,且AM=