题目内容
若椭圆两准线间的距离等于焦距的4倍,则此椭圆的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据题意得出2
=4×2c,即可得出离心率大小.
| a2 |
| c |
解答:
解:∵椭圆两准线间的距离等于焦距的4倍,
∴2
=4×2c,
即
=
,
∴e=
,
故选;D
∴2
| a2 |
| c |
即
| c2 |
| a2 |
| 1 |
| 4 |
∴e=
| 1 |
| 2 |
故选;D
点评:本题考查了椭圆的方程,几何性质的运用,属于容易题,难度不大.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
在△ABC中,A=60°,b=1,S△ABC=
,则
的值为( )
| 3 |
| a |
| sinA |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
若有一组数据的总偏差平方和为120,相关指数为0.6,则回归平方和为( )
| A、60 | B、72 | C、48 | D、120 |
f(x)=xlnx在(0,+∞)上的最小值为( )
| A、e-1 |
| B、-e-1 |
| C、-1 |
| D、不存在 |
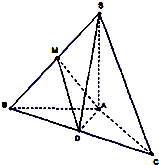 如图,在三棱锥S-ABC中,SA⊥平面ABC,AB=AC=1,SA=2,D为BC的中点.M为SB上的点,且AM=
如图,在三棱锥S-ABC中,SA⊥平面ABC,AB=AC=1,SA=2,D为BC的中点.M为SB上的点,且AM=