题目内容
 如图,一段半径为R,圆心角为90°的扇形圆木,欲按图中阴影部分据成横截面为四边形OABC的木材.试问,怎样据才能使截面面积最大?
如图,一段半径为R,圆心角为90°的扇形圆木,欲按图中阴影部分据成横截面为四边形OABC的木材.试问,怎样据才能使截面面积最大?考点:三角函数的最值,扇形面积公式
专题:计算题,三角函数的求值
分析:以OA和OB分别为x和y轴建立坐标系,A(R,0),C(0,R),设B(Rcosα,Rsinα),则面积=
(cosα+sinα)=
sin(α+
),即可求得结论.
| R2 |
| 2 |
| 2 |
| π |
| 4 |
解答:
解:以OA和OB分别为x和y轴建立坐标系,A(R,0),C(0,R)
圆方程是x2+y2=R2,所以设B(Rcosα,Rsinα)
则面积=
(cosα+sinα)=
sin(α+
)
所以α=
时最大
所以B是弧AC中点时最大,最大面积为
圆方程是x2+y2=R2,所以设B(Rcosα,Rsinα)
则面积=
| R2 |
| 2 |
| 2 |
| π |
| 4 |
所以α=
| π |
| 4 |
所以B是弧AC中点时最大,最大面积为
| 2 |
点评:本题考查利用数学知识解决实际问题,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
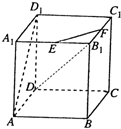 如图,正方体AC1中,E,F分别是A1B1,B1C1的中点.
如图,正方体AC1中,E,F分别是A1B1,B1C1的中点.