题目内容
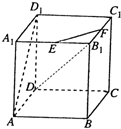 如图,正方体AC1中,E,F分别是A1B1,B1C1的中点.
如图,正方体AC1中,E,F分别是A1B1,B1C1的中点.(Ⅰ)求异面直线DB1与EF所成角的大小;
(Ⅱ)求异面直线AD1与EF所成角的大小.
考点:异面直线及其所成的角
专题:空间角,空间向量及应用
分析:(Ⅰ)分别以DA,DC,DD1所在直线为x轴,y轴,z轴建立空间直角坐标系,然后求出向量
,
的坐标,求这两向量的夹角即能得到异面直线DB1,EF所成角;
(Ⅱ)求出向量AD1的坐标,然后求向量
,
的夹角,这样即可得到异面直线AD1,EF的夹角.
| DB1 |
| EF |
(Ⅱ)求出向量AD1的坐标,然后求向量
| AD1 |
| EF |
解答:
解:如图,分别以边DA,DC,DD1所在直线为x轴,y轴,z轴建立空间直角坐标系D-xyz;
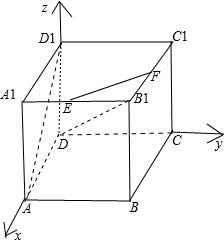 设正方体的边长为1,则可确定以下几点坐标:
设正方体的边长为1,则可确定以下几点坐标:
D(0,0,0),B1((1,1,1),E(1,
,1),F(
,1,1),A(1,0,0),D1(0,0,1);
∴
=(1,1,1),
=(-
,
,0),
=(-1,0,1);
∴(Ⅰ)cos<
,
>=
=0;
∴向量
,
的夹角为90°;
∴异面直线DB1,EF所成角为90°;
(Ⅱ)cos<
,
>=
=
=
;
∴向量
,
夹角为60°;
∴异面直线AD1与EF所成角为60°.
 设正方体的边长为1,则可确定以下几点坐标:
设正方体的边长为1,则可确定以下几点坐标:D(0,0,0),B1((1,1,1),E(1,
| 1 |
| 2 |
| 1 |
| 2 |
∴
| DB1 |
| EF |
| 1 |
| 2 |
| 1 |
| 2 |
| AD1 |
∴(Ⅰ)cos<
| DB1 |
| EF |
| ||||
|
|
∴向量
| DB1 |
| EF |
∴异面直线DB1,EF所成角为90°;
(Ⅱ)cos<
| AD1 |
| EF |
| ||||
|
|
| ||||||
|
| 1 |
| 2 |
∴向量
| AD1 |
| EF |
∴异面直线AD1与EF所成角为60°.
点评:考查通过建立空间直角坐标系,利用空间向量求解异面直线所成角的方法,由点的坐标求向量的坐标,以及向量夹角的余弦公式的坐标运算.

练习册系列答案
相关题目
若集合A={x|-1≤2x+1≤3},B={x|
≤0},则A∩B=( )
| x-2 |
| x |
| A、{x|-1≤x<0} |
| B、{x|-1≤x<0} |
| C、{x|0≤x≤2} |
| D、{x|0<x≤1} |
 如图,一段半径为R,圆心角为90°的扇形圆木,欲按图中阴影部分据成横截面为四边形OABC的木材.试问,怎样据才能使截面面积最大?
如图,一段半径为R,圆心角为90°的扇形圆木,欲按图中阴影部分据成横截面为四边形OABC的木材.试问,怎样据才能使截面面积最大?