题目内容
已知一列数1,2,4,7,11,16,…n,按照这个顺序下去,求前n项和.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:由题意可得第n个数an=1+1+2+3+…+(n-1)=1+
=
n2-
n+1,故可求得前n项和.
| n(n-1) |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:1=1,
2=1+1,
4=1+1+2,
7=1+1+2+3,
11=1+1+2+3+4,
…
∴第n个数an=1+1+2+3+…+(n-1)=1+
=
n2-
n+1,
∴Sn=
(12+22+…+n2)-
(1+2+3+…+n)+n=
×
-
×
+n=
.
2=1+1,
4=1+1+2,
7=1+1+2+3,
11=1+1+2+3+4,
…
∴第n个数an=1+1+2+3+…+(n-1)=1+
| n(n-1) |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴Sn=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| n(n+1)(2n+1) |
| 6 |
| 1 |
| 2 |
| n(n+1) |
| 2 |
| n3+5n |
| 6 |
点评:本题考查递推数列求通项公式及数列求和知识,考查学生的运算求解能力,属于中档题.

练习册系列答案
相关题目
下列四组不等式中,不同解的是( )
A、
| ||
| B、|x-3|>|2x+6|(x∈R) 与 (x-3)2>(2x+6)2 | ||
C、
| ||
D、
|
一个四棱锥的三视图如图所示,其侧视图是等边三角形,该四棱锥的体积等于( )
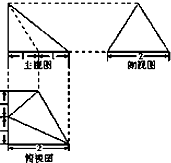

A、
| ||
B、2
| ||
C、3
| ||
D、6
|