Question

圆锥底面半径为1cm，高为

2

cm，其中有一个内接正方体．
（1）画出轴截面中截正方体的截面面积最大的截面图形；
（2）求这个内接正方体的棱长．

Answer 1

考点：棱柱、棱锥、棱台的体积

专题：空间位置关系与距离

分析：（1）先做出示意图，再作轴截面中截正方体的截面面积最大的截面图形．
（2）设OO₁=A₁B₁=x，则A₁O₁=

x

2

，从而

x 2

2 -x

=

1

2

，由此能求出这个内接正方体的棱长．

解答： 解：（1）由已知得示意图为：

∴轴截面中截正方体的截面面积最大的截面图形为：

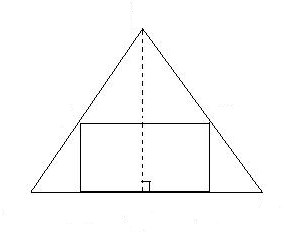
（2）如图，已知OA=1，OP=

2

，设OO₁=A₁B₁=x，
A₁O₁=

x

2

，

A1O1

O1P

=

AO

OP

，

x 2

2 -x

=

1

2

，
∴

x

2- 2 x

=

1

2

，
解得x=

2

2

，
故这个内接正方体的棱长为

2

2

．

点评：本题考查轴截面中截正方体的截面面积最大的截面图形的作法，考查这个内接正方体的棱长的求法，解题时要认真审题，注意空间思维能力的培养．