题目内容
已知|
|=4,|
|=5,<
,
>=
,(
+
)•
= .
| a |
| b |
| a |
| b |
| π |
| 3 |
| a |
| b |
| a |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:运用向量的数量积的定义和性质,即斜率的平方即为模的平方,即可得到所求值.
解答:
解:由于|
|=4,|
|=5,<
,
>=
,
则
•
=4×5×cos
=10,
则有(
+
)•
=
2+
•
=16+10=26.
故答案为:26
| a |
| b |
| a |
| b |
| π |
| 3 |
则
| a |
| b |
| π |
| 3 |
则有(
| a |
| b |
| a |
| a |
| a |
| b |
=16+10=26.
故答案为:26
点评:本题考查平面向量的数量积的定义和性质,考查向量的平方即为模的平方,考查运算能力,属于基础题.

练习册系列答案
相关题目
(1)已知不等式x2+bx+c>0的解集是{x|x<2或x>3},求b、c的值;
(2)已知二次不等式ax2+bx+c<0的解集为{x|x<
或x>
},求关于x的不等式cx2-bx+a>0的解集.
(2)已知二次不等式ax2+bx+c<0的解集为{x|x<
| 1 |
| 3 |
| 1 |
| 2 |
已知向量
,
满足
﹒
=0,且|
|=1,
|=2则,则|
-2
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、2 | ||
B、
| ||
| C、4 | ||
| D、5 |
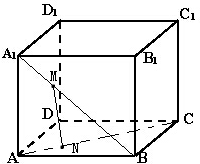 已知正方体ABCD-A1B1C1D1的棱长为a,M、N分别为A1B和AC上的点,A1M=AN=
已知正方体ABCD-A1B1C1D1的棱长为a,M、N分别为A1B和AC上的点,A1M=AN=