题目内容
圆ρ=2cosθ被极轴及直线θ=
(ρ∈R)所截取的面积为 .
| π |
| 4 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:首先,根据圆ρ=2cosθ,得(x-1)2+y2=1,然后,根据直线θ=
(ρ∈R),得到y=x,所求面积为:圆被直线y=x和x轴所截得的部分为:圆的
和一个腰为1的等腰直角三角形,然后,求解即可.
| π |
| 4 |
| 1 |
| 4 |
解答:
解:根据圆ρ=2cosθ,得
x2+y2=2x,
∴(x-1)2+y2=1,
∵直线θ=
(ρ∈R),
∴y=x,
圆被直线y=x和x轴所截得的部分为:圆的
和一个腰为1的等腰直角三角形,
∴S=
+
.
故答案为:
+
.
x2+y2=2x,
∴(x-1)2+y2=1,
∵直线θ=
| π |
| 4 |
∴y=x,
圆被直线y=x和x轴所截得的部分为:圆的
| 1 |
| 4 |
∴S=
| π |
| 4 |
| 1 |
| 2 |
故答案为:
| π |
| 4 |
| 1 |
| 2 |
点评:本题重点考查了直线的极坐标方程和圆的极坐标方程、面积的求解等知识,属于中档题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
已知平面向量
,
(α≠0,α≠β)满足|
|=1,且
与
-
的夹角为120°,则|
|的取值范围是( )
| α |
| β |
| β |
| α |
| β |
| α |
| α |
A、[0,
| ||||
B、[0,
| ||||
C、(0,
| ||||
D、(
|
设四面体ABCD的六条棱的长分别为1,1,
,
,
和
,则其外接球的表面积为( )
| 2 |
| 2 |
| 2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,若圆C:(x+1)2+y2=36上的动点M与点B(1,0)连线的垂直平分线与CM交于点G,则点G的轨迹方程是
如图,若圆C:(x+1)2+y2=36上的动点M与点B(1,0)连线的垂直平分线与CM交于点G,则点G的轨迹方程是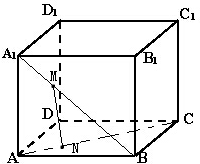 已知正方体ABCD-A1B1C1D1的棱长为a,M、N分别为A1B和AC上的点,A1M=AN=
已知正方体ABCD-A1B1C1D1的棱长为a,M、N分别为A1B和AC上的点,A1M=AN=