题目内容
若函数f(x)=
为奇函数,求a的值.
| 2x+a |
| 2x-a |
考点:有理数指数幂的化简求值
专题:计算题,函数的性质及应用
分析:由题意可得f(-x)+f(x)=0,化简可得2•2x(1-a2)=0,从而可得a=1或a=-1;检验即可.
解答:
解:∵函数f(x)=
为奇函数,
∴f(-x)+f(x)=0,
即
+
=0,
化简得,
+
=0,
故(1+a•2x)(2x-a)+(1-a2x)(2x+a)=0;
故2•2x(1-a2)=0,
解得,a=1或a=-1;
若a=1,f(x)=
为(-∞,0)∪(0,+∞)上奇函数,
若a=-1,则f(x)=
是R上的奇函数.
故a=1或a=-1.
| 2x+a |
| 2x-a |
∴f(-x)+f(x)=0,
即
| 2-x+a |
| 2-x-a |
| 2x+a |
| 2x-a |
化简得,
| 1+a2x |
| 1-a2x |
| 2x+a |
| 2x-a |
故(1+a•2x)(2x-a)+(1-a2x)(2x+a)=0;
故2•2x(1-a2)=0,
解得,a=1或a=-1;
若a=1,f(x)=
| 2x+1 |
| 2x-1 |
若a=-1,则f(x)=
| 2x-1 |
| 2x+1 |
故a=1或a=-1.
点评:本题考查了函数的性质的应用,属于基础题.

练习册系列答案
相关题目
已知P(4,-9),Q(-2,3),y轴与线段PQ的交点为M,则M分
所成的比为( )
| PQ |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
已知平面向量
,
(α≠0,α≠β)满足|
|=1,且
与
-
的夹角为120°,则|
|的取值范围是( )
| α |
| β |
| β |
| α |
| β |
| α |
| α |
A、[0,
| ||||
B、[0,
| ||||
C、(0,
| ||||
D、(
|
 如图,若圆C:(x+1)2+y2=36上的动点M与点B(1,0)连线的垂直平分线与CM交于点G,则点G的轨迹方程是
如图,若圆C:(x+1)2+y2=36上的动点M与点B(1,0)连线的垂直平分线与CM交于点G,则点G的轨迹方程是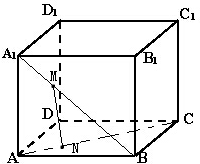 已知正方体ABCD-A1B1C1D1的棱长为a,M、N分别为A1B和AC上的点,A1M=AN=
已知正方体ABCD-A1B1C1D1的棱长为a,M、N分别为A1B和AC上的点,A1M=AN=