题目内容
13．已知空间几何体的三视图如图所示，则该几何体的体积是$\frac{8}{3}$．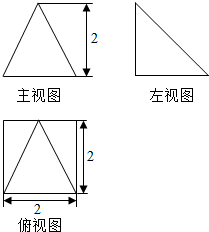
分析 由已知中的三视图可得：该几何体是一个以俯视图为底面的四棱锥，代入棱锥体积公式，可得答案．
解答 解：由已知中的三视图可得：该几何体是一个以俯视图为底面的四棱锥，
棱锥的底面面积S=2×2=4，
棱锥的高h=2，
故棱锥的体积V=$\frac{1}{3}Sh$=$\frac{8}{3}$；
故答案为：$\frac{8}{3}$
点评 本题考查的知识点是由三视图，求体积和表面积，根据已知的三视图，判断几何体的形状是解答的关键．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
4．圆O：x2+y2-2x-7=0与直线l：（λ+1）x-y+1-λ=0（λ∈R）的位置关系是（ ）
| A． | 相切 | B． | 相交 | C． | 相离 | D． | 不确定 |
4．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的左、右焦点分别为F1、F2，P为椭圆上一点，连接PF1交y轴于点Q，若△PQF2为等边三角形，则椭圆C的离心率为（ ）
| A． | $\frac{{\sqrt{2}}}{2}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $\frac{{\sqrt{3}}}{3}$ | D． | $\frac{{\sqrt{6}}}{3}$ |
1．已知A，B是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的两个顶点，若P双曲线上一点，P关于x轴对称点为Q，若直线AP，BQ的斜率分别K1，K2且K1K2=-$\frac{4}{9}$，则该双曲线的离心率为（ ）
| A． | $\sqrt{5}$ | B． | $\frac{\sqrt{5}}{3}$ | C． | $\frac{\sqrt{13}}{2}$ | D． | $\frac{\sqrt{13}}{3}$ |
向高为H的水瓶A、B、C、D中同时以等速注水，注满为止，若水量V与水深h的函数的图象如图，则水瓶的形状为（ ）
已知O为坐标原点，向量$\overrightarrow{OA}$=（3cosx，3sinx），$\overrightarrow{OB}$=（3cosx，sinx），$\overrightarrow{OC}$=（$\sqrt{3}$，0），x∈（0，$\frac{π}{2}$）．