题目内容
函数f(x)=-x3+ax2(a∈R).
(1)当a>0时,求函数y=f(x)的极值;
(2)若x∈[0,1]时,函数y=f(x)图象上任意一点处的切线倾斜角为θ,求当0≤θ≤
时a的取值范围.
(1)当a>0时,求函数y=f(x)的极值;
(2)若x∈[0,1]时,函数y=f(x)图象上任意一点处的切线倾斜角为θ,求当0≤θ≤
| π |
| 4 |
考点:利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)由f′(x)=-3x2+2ax,令f′(x)=0,得x=0,或x=
a.a>0.利用导数与单调性的关系列出表格即可得出.
(2)当x∈[0,1]时,tanθ=f′(x)=-3x2+2ax,由θ∈[0,
],得0≤f′(x)≤1,即x∈[0,1]时,0≤-3x2+2ax≤1恒成立.对x分类讨论,分离参数,利用基本不等式的性质即可得出.
| 2 |
| 3 |
(2)当x∈[0,1]时,tanθ=f′(x)=-3x2+2ax,由θ∈[0,
| π |
| 4 |
解答:
解:(1)由f′(x)=-3x2+2ax,令f′(x)=0,得x=0,或x=
a.a>0.
∴当x变化时,f′(x)、f(x)的变化情况如下表:
∴y极小值=f(0)=0.y极大值=f(
a)=-
a3+
a3=
a3.
(2)当x∈[0,1]时,tanθ=f′(x)=-3x2+2ax,由θ∈[0,
],得0≤f′(x)≤1,
即x∈[0,1]时,0≤-3x2+2ax≤1恒成立.
当x=0时,a∈R.
当x∈(0,1]时,由-3x2+2ax≥0恒成立,可知a≥
.
由-3x2+2ax≤1恒成立,得a≤
(3x+
),∴a≤
(等号在x=
时取得).
综上:
≤a≤
.
| 2 |
| 3 |
∴当x变化时,f′(x)、f(x)的变化情况如下表:
| x | (-∞,0) | 0 | (0,
|
| (
| ||||||
| f′(x) | - | 0 | + | 0 | - | ||||||
| f(x) | 单调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
| 2 |
| 3 |
| 8 |
| 27 |
| 4 |
| 9 |
| 4 |
| 27 |
(2)当x∈[0,1]时,tanθ=f′(x)=-3x2+2ax,由θ∈[0,
| π |
| 4 |
即x∈[0,1]时,0≤-3x2+2ax≤1恒成立.
当x=0时,a∈R.
当x∈(0,1]时,由-3x2+2ax≥0恒成立,可知a≥
| 3 |
| 2 |
由-3x2+2ax≤1恒成立,得a≤
| 1 |
| 2 |
| 1 |
| x |
| 3 |
| ||
| 3 |
综上:
| 3 |
| 2 |
| 3 |
点评:本题考查了利用导数研究函数的单调性极值、几何意义、基本不等式的性质,考查了分类讨论、分离参数方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
过原点的直线交双曲线x2-y2=4
于P,Q两点,现将坐标平面沿直线y=-x折成直二面角,则折后PQ长度的最小值等于( )
| 2 |
A、2
| ||
| B、4 | ||
C、4
| ||
D、3
|
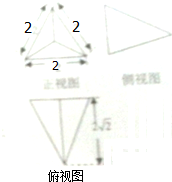
已知三棱锥的三视图,则该三棱锥的体积是( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图所示,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等腰梯形,等腰直角三角形和长方形,则该几何体表面积为( )
如图所示,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等腰梯形,等腰直角三角形和长方形,则该几何体表面积为( )| A、14 | ||
B、14+2
| ||
C、8+8
| ||
| D、16 |
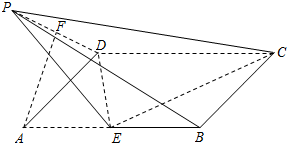 如图所示,在矩形ABCD中,AD=1,AB=2,点E是线段AB的中点,把三角形AED沿DE折起,设折起后点A的位置为 P,F是PD的中点.
如图所示,在矩形ABCD中,AD=1,AB=2,点E是线段AB的中点,把三角形AED沿DE折起,设折起后点A的位置为 P,F是PD的中点.