题目内容
已知函数f（x）=loga（x+1），g（x）=loga（1-x）（a＞0且a≠1），令F（x）=f（x）-g（x）．
（1）求函数y=F（x）的定义域；
（2）判断函数y=F（x）的奇偶性并说明理由．
（1）求函数y=F（x）的定义域；
（2）判断函数y=F（x）的奇偶性并说明理由．
考点：对数函数的图像与性质,函数的定义域及其求法
专题：
分析：（1）根据对数函数衬里的条件建立不等式组解不等式组求得结果．
（2）判定函数的奇偶性要注意两个条件①定义域所在的区间数否对称②是否满足f（-x）=±（x）．
（2）判定函数的奇偶性要注意两个条件①定义域所在的区间数否对称②是否满足f（-x）=±（x）．
解答：
解：（1）函数f（x）=loga（x+1），g（x）=loga（1-x）（a＞0且a≠1），
令F（x）=f（x）-g（x）．
依题意得
解得：-1＜x＜1
∴定义域为{x|-1＜x＜1}
（2）根据（1）的结论：
所以：①x∈（-1，1），
②F（-x）=loga（1-x）-loga（1+x）=-F（x）
∴F（x）为奇函数．
令F（x）=f（x）-g（x）．
依题意得
|
解得：-1＜x＜1
∴定义域为{x|-1＜x＜1}
（2）根据（1）的结论：
所以：①x∈（-1，1），
②F（-x）=loga（1-x）-loga（1+x）=-F（x）
∴F（x）为奇函数．
点评：本题考查的知识要点：函数定义域的求法，函数奇偶性的判定，属于基础题型．
练习册系列答案
相关题目
某三棱锥的三视图如图所示，该三棱锥四个面的面积中最大的是（ ）
A、2
| ||
| B、12 | ||
C、8
| ||
D、6
|
已知|
+
|=
，|
-
|=
，|
|=2，则|
|=（ ）
| a |
| b |
| 19 |
| a |
| b |
| 7 |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
| D、3 |
有一个所有棱长均为a的正四棱锥P-ABCD，还有一个所有棱长均为a的正三棱锥．将此三棱锥的一个面与正四棱锥的一个侧面完全重合地粘在一起，得到一个如图所示的多面体．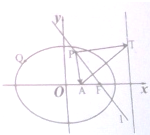
如图，Q为椭圆E：