题目内容
解方程组
.
|
考点:根式与分数指数幂的互化及其化简运算
专题:圆锥曲线的定义、性质与方程
分析:由方程的几何意义根据坐标轴旋转得到方程组在新系下的方程,联立后求得交点坐标,还原后得答案.
解答:
解:方程
=1+
的几何意义为动点(a,b)到定点(1,0)的距离等于动点(a,b)到定直线a+
b=0的距离加1,
令
,
则定点(1,0)化为(
,
),定直线a+
b=0化为b′=0,
则方程
=1+
在新坐标系下的方程为(a′-
)2=
(b′-
) ①,
方程
=
化为:a′=2
②,
联立①②得:
.
则a=
a′+
b′=
,b=
b′-
a′=
.
∴原方程组的解为
.
| (a-1)2+b2 |
|a+
| ||
| 2 |
| 3 |
令
|
则定点(1,0)化为(
| ||
| 2 |
| 1 |
| 2 |
| 3 |
则方程
| (a-1)2+b2 |
|a+
| ||
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
方程
b+
| ||
| a-3 |
| 3 |
| 3 |
联立①②得:
|
则a=
| ||
| 2 |
| 1 |
| 2 |
| 45 |
| 8 |
| ||
| 2 |
| 1 |
| 2 |
13
| ||
| 8 |
∴原方程组的解为
|
点评:本题考查了抛物线的几何意义,考查了坐标轴旋转问题,体现了数学转化思想方法,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
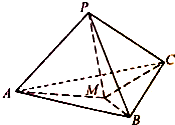 如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3,PB=2,PC=1.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=(
如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3,PB=2,PC=1.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=(