Question

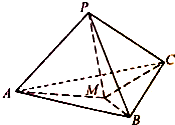如图，在三棱锥P-ABC中，PA、PB、PC两两垂直，且PA=3，PB=2，PC=1．设M是底面ABC内一点，定义f（M）=（m，n，p），其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积．若f（M）=（

1

2

，x，y），若

1

y

+

a

x

≥8恒成立，求a取值范围．

Answer 1

考点：棱柱、棱锥、棱台的体积

专题：空间位置关系与距离

分析：先根据三棱锥的特点求出其体积，然后利用基本不等式求出

1

y

+

a

x

的最值，建立关于a的不等关系，解之即可．

解答： 解：∵PA、PB、PC两两垂直，且PA=3．PB=2，PC=1．
∴V _P-ABC=

1

3

×

1

2

×3×2×1=1=

1

2

+x+y，
即x+y=

1

2

，则2x+2y=1，

1

y

+

a

x

=（

1

y

+

a

x

）（2x+2y）=

2x

y

+2a+2+

2ay

x

≥2+2a+4

a

≥8，
解得a≥1或a≤-3（舍）
∴实数a的取值范围是[1，+∞）．

点评：本题主要考查了棱锥的体积，同时考查了基本不等式的运用，是题意新颖的一道题目，属于中档题．