题目内容
已知关于x的一次函数y=kx+b.
(Ⅰ)设集合P={-2,-1,2,3}和Q={-2,2,3},其中k∈P,b∈Q,求函数y=kx+b在R上是增函数的概率;
(Ⅱ)实数k,b满足条件
,求函数y=kx+b的图象经过一、三、四象限的概率(边界及坐标轴的面积忽略不计).
(Ⅰ)设集合P={-2,-1,2,3}和Q={-2,2,3},其中k∈P,b∈Q,求函数y=kx+b在R上是增函数的概率;
(Ⅱ)实数k,b满足条件
|
考点:简单线性规划
专题:不等式的解法及应用,概率与统计
分析:(Ⅰ)列出满足条件的所有基本事件总数,写出所求基本知识的个数,即可求解概率.
(Ⅱ)画出约束条件的
,可行域,然后求解函数y=kx+b的图象经过一、三、四象限的概率.
(Ⅱ)画出约束条件的
|
解答:
 解:(Ⅰ)抽取的全部结果的基本事件有:(-2,-2),(-2,2),(-2,3),
解:(Ⅰ)抽取的全部结果的基本事件有:(-2,-2),(-2,2),(-2,3),
(-1,-2),(-1,2),(-1,3),(2,-2),(2,2),(2,3),(3,-2),(3,2),(3,3)共12个基本事件. …(2分)
设使函数为增函数的事件为A,则A包含的基本事件有:(2,-2),(2,2),
(2,3),(3,-2),(3,2),(3,3),共6个基本事件,…(4分)
所以,P(A)=
=
.…(6分)
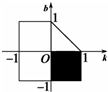
(Ⅱ)实数k,b满足条件
的区域如图所示,…(8分)
要使函数的图象过一、三、四象限,则k>0,b<0,故使函数图象过一、三、四象限的(k,b)的区域为第四象限的阴影部分,…(10分)
∴所求事件的概率为p=
.…(12分)
 解:(Ⅰ)抽取的全部结果的基本事件有:(-2,-2),(-2,2),(-2,3),
解:(Ⅰ)抽取的全部结果的基本事件有:(-2,-2),(-2,2),(-2,3),(-1,-2),(-1,2),(-1,3),(2,-2),(2,2),(2,3),(3,-2),(3,2),(3,3)共12个基本事件. …(2分)
设使函数为增函数的事件为A,则A包含的基本事件有:(2,-2),(2,2),
(2,3),(3,-2),(3,2),(3,3),共6个基本事件,…(4分)
所以,P(A)=
| 6 |
| 12 |
| 1 |
| 2 |
(Ⅱ)实数k,b满足条件
|
要使函数的图象过一、三、四象限,则k>0,b<0,故使函数图象过一、三、四象限的(k,b)的区域为第四象限的阴影部分,…(10分)
∴所求事件的概率为p=
| 2 |
| 7 |
点评:本题考查简单的线性规划,以及古典概型和几何概型的应用,考查计算能力.

练习册系列答案
相关题目
已知cos(θ+
)=-
,θ∈(0,
),则cos2θ=( )
| π |
| 4 |
| ||
| 10 |
| π |
| 2 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
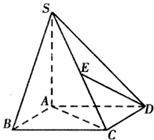 已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,SA=AB=AD=2,
已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,SA=AB=AD=2,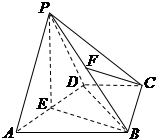 如图,在四棱锥P-ABCD中,侧面PAD是等边三角形,AB∥CD,AB=2CD,BC⊥CD,∠DBC=30°,点E,F分别为AD,PB的中点.
如图,在四棱锥P-ABCD中,侧面PAD是等边三角形,AB∥CD,AB=2CD,BC⊥CD,∠DBC=30°,点E,F分别为AD,PB的中点.