题目内容
已知向量a＝(sinα，－2)，b＝(1，cosα)，其中α∈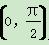
.
(1)向量a，b能平行吗？请说明理由．
(2)若a⊥b，求sinα和cosα的值．
(3)在(2)的条件下，若cosβ＝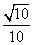
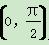，β∈，求α＋β的值．
解 (1)向量a，b不能平行．若平行，需sinαcosα＋2＝0，
即sin2α＝－4，而－4∉[－1,1]，∴向量a，b不能平行．
(2)∵a⊥b，∴a·b＝sinα－2cosα＝0，
即sinα＝2cosα，又∵sin2α＋cos2α＝1，
∴4cos2α＋cos2α＝1，即cos2α＝
，∴sin2α＝
，
又α∈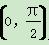，∴sinα＝
，cosα＝
.
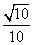(3)由(2)知sinα＝，cosα＝，cosβ＝，β∈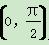，得sinβ＝
.
则cos(α＋β)＝cosαcosβ－sinαsinβ＝×－×＝－
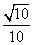.又α＋β∈(0，π)，则α＋β＝
.
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
的图象向右平移
个单位，再把所得图象上各点的横坐标缩短到原来的一半，则所得图象对应的函数解析式是( )
B．y＝sin
B．2－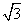
对于平面ABC上任意一点O，动点P满足
＋λa＋λb，则动点P的轨迹所过的定点为________．
＝(1，－3)，
＝(2，－1)，
＝(k＋1，k－2)，若A，B，C三点不能构成三角形，则实数k应满足的条件是( )
，且a⊥(a＋b)，则a与b的夹角为( )
＝(1，－3)，|
|，
|＝________.
若
＋z2是实数，求实数a的值．