题目内容
15.将A,B,C,D,E排成一列,要求A,B,C在排列中顺序为“A,B,C”或“C,B,A”( A,B,C可以不相邻),这样的排列数有( )| A. | 12种 | B. | 20种 | C. | 40种 | D. | 60种 |
分析 解:根据题意,分三人按“A,B,C”的顺序和按“C,B,A”的顺序2种情况讨论,利用插空法分析每一种情况下安排方法的数目,由分类计数原理计算可得答案.
解答 解:根据题意,分2种情况讨论:
①、三人按“A,B,C”的顺序排列,排好后有4个空位,
在4个空位中选1个安排D,有4种选法,4人排好后有5个空位,
在5个空位中选1个安排E,有5种选法,
则一共有4×5=20种安排方法,
②、三人按“C,B,A”的顺序排列,
同理,此时有20种排列方法;
综合可得:这样的排列有20+20=40种;
故选:C.
点评 本题考查排列、组合的应用,注意DE没有相邻或不相邻的要求.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
3.某医院拟派2名内科医生、3名外科医生和3名护士共8人组成两个医疗分队,平均分到甲、乙两个村进行义务巡诊,其中每个分队都必须有内科医生、外科医生和护士,则不同的分配方案有( )
| A. | 72 | B. | 36 | C. | 24 | D. | 18 |
4.设集合A={x|x2-x-6≤0},$B=\{x|\sqrt{x^2}>2\}$,则A∩B=( )
| A. | (2,3] | B. | (2,3) | C. | (-2,3] | D. | (-2,3) |
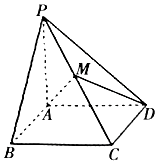 如图所示,已知四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC的中点.
如图所示,已知四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC的中点.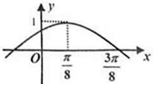 函数f(x)=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的单调递减区间为[$\frac{π}{4}+kπ$,$\frac{5π}{8}+kπ$],k∈Z.
函数f(x)=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的单调递减区间为[$\frac{π}{4}+kπ$,$\frac{5π}{8}+kπ$],k∈Z.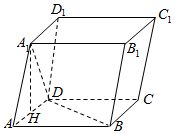 四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AD=AA1=A1D=2,H为AD中点,且A1H⊥BD.
四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AD=AA1=A1D=2,H为AD中点,且A1H⊥BD.