题目内容
已知实数a≠0,集合A={x|y=ln
},B={x|2<x<4}.
(1)求集合A;
(2)设命题p:x∈A.,命题q:x∈B,若p是q成立的必要条件,求实数a的取值范围.
| ax |
| x-a2-1 |
(1)求集合A;
(2)设命题p:x∈A.,命题q:x∈B,若p是q成立的必要条件,求实数a的取值范围.
考点:必要条件、充分条件与充要条件的判断
专题:函数的性质及应用
分析:根据a的正负,求出集合A,在根据集合之间的包含关系即可求出a的取值范围.
解答:
解:(1)当a>0时,由
>0,?x<0或x>a2+1,∴A=(-∞,0)∪(a2+1,+∞)
当a<0时,由
.>0?0<x<a2+1,∴A=(0,a2+1)
(2)命题p:x∈A.,命题q:x∈B,若p是q成立的必要条件,则q⇒p,则B⊆A.又B={x|2<x<4}.
当a>0时,a2+1≤2,∴0<a≤1;当a<0时,a2+1≥4,∴a≤-
综上,a的取值范围是(-∞,-
]∪(0,1)
| ax |
| x-a2-1 |
当a<0时,由
| ax |
| x-a2-1 |
(2)命题p:x∈A.,命题q:x∈B,若p是q成立的必要条件,则q⇒p,则B⊆A.又B={x|2<x<4}.
当a>0时,a2+1≤2,∴0<a≤1;当a<0时,a2+1≥4,∴a≤-
| 3 |
综上,a的取值范围是(-∞,-
| 3 |
点评:本题以充分必要条件为载体,考查了集合之间的包含关系,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=
,则下列结论正确的是( )
|
| A、f(x)是偶函数 |
| B、f(x)在f(x)上是增函数 |
| C、f(x)是周期函数 |
| D、f(x)的值域为[-1,+∞) |
| 2cos20°-1 |
| cos20°sin220° |
A、
| ||
B、2-
| ||
| C、4 | ||
| D、8 |
已知函数f(x+1)是偶函数,当x∈(-∞,1)时,函数f(x)单调递减,设a=f(-
),b=f(-1),c=f(2),a=f(-
),b=f(-1),c=f(2),则a,b,c的大小关系为 .
| 1 |
| 2 |
| 1 |
| 2 |
方程x3-x-3=0的实数解所在的区间是( )
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
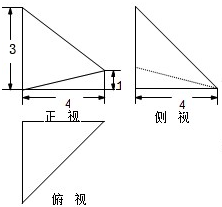 已知一个几何体的三视图如图所示,其中正视图是直角梯形.
已知一个几何体的三视图如图所示,其中正视图是直角梯形.