题目内容
若a=20.5,b=logπ3,c=log
e,则( )
| 1 |
| 2 |
| A、a>b>c |
| B、b>a>c |
| C、c>a>b |
| D、b>c>a |
考点:对数值大小的比较
专题:函数的性质及应用
分析:利用对数函数和指数函数的性质求解.
解答:
解:∵a=20.5=
>1,
0=logπ1<b=logπ3<logππ=1,
c=log
e<log
1=0,
∴a>b>c.
故选:A.
| 2 |
0=logπ1<b=logπ3<logππ=1,
c=log
| 1 |
| 2 |
| 1 |
| 2 |
∴a>b>c.
故选:A.
点评:本题考查三个数的大小的求法,是基础题,解题时要认真审题,注意对数函数和指数函数的性质的合理运用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
| 1+2i |
| 1+i |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
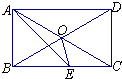 如图,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则以下结论:①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE,⑤∠AEO=30°其中正确的有( )
如图,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则以下结论:①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE,⑤∠AEO=30°其中正确的有( )| A、1个 | B、2个 | C、3个 | D、4个 |
在△ABC中,tanA=
,cosB=
,则sinC=( )
| 1 |
| 2 |
3
| ||
| 10 |
A、
| ||||
| B、1 | ||||
C、
| ||||
| D、-2 |
已知向量
、
满足:|
|=2|
|=2
•
=2,若
-
与
-
的夹角等于
,则
•
的最大值为( )
| a |
| b |
| b |
| a |
| a |
| b |
| c |
| a |
| c |
| b |
| π |
| 2 |
| c |
| a |
A、
| ||||
B、
| ||||
C、1+
| ||||
D、1+
|
函数y=
的值域是( )
| 25-5x |
| A、[0,+∞) |
| B、[0,5] |
| C、[0,5) |
| D、(0,5) |