题目内容
已知向量
=(cosx,sin(
+x)),
=(2
sinx,2cosx).
(Ⅰ)若
≠0,
∥
,求tan2x的值;
(Ⅱ)设函数f(x)=
•
,求函数f(x)的最大值及取得最大值时x的集合.
| m |
| π |
| 2 |
| n |
| 3 |
(Ⅰ)若
| m |
| m |
| n |
(Ⅱ)设函数f(x)=
| m |
| n |
考点:平面向量数量积的运算,平面向量共线(平行)的坐标表示
专题:三角函数的求值,三角函数的图像与性质,平面向量及应用
分析:(Ⅰ)由向量共线的坐标表示和诱导公式,结合同角的商数关系和二倍角的正切公式,计算即可得到;
(Ⅱ)运用向量的数量积的坐标表示,由二倍角的正弦、余弦公式和两角和的正弦公式,结合正弦函数的值域即可得到最大值和x的集合.
(Ⅱ)运用向量的数量积的坐标表示,由二倍角的正弦、余弦公式和两角和的正弦公式,结合正弦函数的值域即可得到最大值和x的集合.
解答:
解:(Ⅰ)向量
=(cosx,sin(
+x)),
=(2
sinx,2cosx).
若
≠0,
∥
,则2cos2x=2
sinxsin(
+x),
即cos2x=
sinxcosx,(cosx≠0),
即有tanx=
,
tan2x=
=
=
;
(Ⅱ)函数f(x)=
•
=2
sinxcosx+2cosxsin(
+x)
=
sin2x+cos2x+1=2sin(2x+
)+1,
当2x+
=2kπ+
,k∈Z,即x=kπ+
,f(x)取得最大值,且为3,
此时x的取值集合为{x|x=x=kπ+
,k∈Z}.
| m |
| π |
| 2 |
| n |
| 3 |
若
| m |
| m |
| n |
| 3 |
| π |
| 2 |
即cos2x=
| 3 |
即有tanx=
| ||
| 3 |
tan2x=
| 2tanx |
| 1-tan2x |
2×
| ||||
1-
|
| 3 |
(Ⅱ)函数f(x)=
| m |
| n |
| 3 |
| π |
| 2 |
=
| 3 |
| π |
| 6 |
当2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
此时x的取值集合为{x|x=x=kπ+
| π |
| 6 |
点评:本题考查向量的数量积的坐标表示,以及向量共线的坐标运算,主要考查诱导公式和二倍角公式及两角和的正弦公式,同时考查正弦函数的最值,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
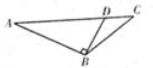
如图,在△ABC中,点D在AC上,AB⊥BD,BC=3
,BD=5,sin∠ABC=
,则CD的长为( )
| 3 |
2
| ||
| 5 |

A、
| ||
| B、4 | ||
C、2
| ||
| D、5 |
设二项式(x-
)4的展开式中常数项为A,则A=( )
| 1 | |||
|
| A、-6 | B、-4 | C、4 | D、6 |
数列{an}满足an+1=
,若a1=
,则a2015=( )
|
| 4 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|



