题目内容
函数f（x）=
的定义域为（ ）
1-
|
| A、（0，1） |
| B、（-∞，0）∪（1，+∞） |
| C、（0，1] |
| D、（-∞，0）∪[1，+∞） |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数的解析式，列出使解析式有意义的不等式组，求出解集即可．
解答：
解：根据题意，得；
，
解得x＜0，或x≥1；
∴函数的定义域是（-∞，0）∪[1，+∞）．
故选：D．
|
解得x＜0，或x≥1；
∴函数的定义域是（-∞，0）∪[1，+∞）．
故选：D．
点评：本题考查了求函数的定义域的问题，解题的关键是应根据函数的解析式，列出使解析式有意义的不等式组，是容易题．
练习册系列答案
孟建平名校考卷系列答案
相关题目
观察如图：则第 行的各数之和等于20092．（ ）| A、1004 | B、1005 |
| C、1006 | D、1007 |
设l，m，n表示不同的直线，α，β，γ表示不同的平面，给出下列四个命题，其中正确的命题是（ ）
| A、若m∥l，且m∥α，则l∥α |
| B、若m∥l，且m⊥α，则l⊥α |
| C、若α∩β=l，β∩γ=m，γ∩α=n，则l∥m∥n |
| D、若α∩β=m且l∥m，则l∥α |
函数y=
的大致图象如图所示，则（ ）
| x |
| x2+a |
| A、a∈（-1，0） |
| B、a∈（0，1） |
| C、a∈（-∞，1） |
| D、a∈（1，+∞） |
正方体的内切球，与各棱相切的球，外接球的体积之比为（ ）
| A、1：2：3 | ||||||
B、1：
| ||||||
C、1：2
| ||||||
D、1：
|
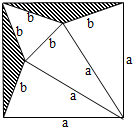如图，把边长为a的正方形剪去图中的阴影部分，沿图中所画的折成一个正三棱锥，则这个正三棱锥的高是（ ）A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
下列命题正确的是（ ）
| A、有一条侧棱与底面两边垂直的棱柱是直棱柱 |
| B、有一个侧面是矩形的棱柱是直棱柱 |
| C、有两个侧面是矩形的棱柱是直棱柱 |
| D、有两个相邻侧面是矩形的棱柱是直棱柱 |
cos（-
）的值为（ ）
| 16π |
| 3 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|