题目内容
5．数列{an}为等比数列，Sn是数列{an}的前n项和，且Sn＞0，a6是a5、a4的等差中项，则数列{an}的公比q为（ ）| A． | -$\frac{1}{2}$或1 | B． | $\frac{1}{2}$或1 | C． | 1 | D． | -$\frac{1}{2}$ |
分析 利用等差数列的性质与等比数列的通项公式即可得出．
解答 解：∵a6是a5、a4的等差中项，
∴2a6=a5+a4
即2a5q=a5+$\frac{{a}_{5}}{q}$，
∵Sn＞0，数列{an}为等比数列，
∴2q=1+$\frac{1}{q}$，
即2q2-q-1=0，
解得q=1，
故选：C，
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式，考查了推理能力和计算能力，属于基础题
练习册系列答案
全能测控期末小状元系列答案
相关题目
15．执行如图所示的程序框图，若输入n=6，则输出的S=（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{7}$ | D． | $\frac{4}{9}$ |
16．下列各式的大小关系正确的是（ ）
| A． | sin11°＞sin168° | B． | sin194°＜cos160° | ||
| C． | tan（-$\frac{π}{5}$）＜tan（-$\frac{3π}{7}$） | D． | cos（-$\frac{15π}{8}$）＞cos$\frac{14π}{9}$ |
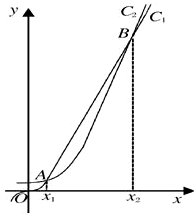函数f（x）=2x和g（x）=x3的部分图象的示意图如图所示．设两函数的图象交于点A（x1，y1）、B（x2，y2），x1＜x2．