题目内容
18.若函数f(x)是定义在R上的奇函数,且满足f(x+2)=-f(x),则f(2016)=0.分析 因为函数f(x)是定义在R上的奇函数,所以有f(0)=0,又因为f(x+2)=-f(x),所以有f(x+4)=-f(x+2)=f(x),所以函数f(x)的周期为4,
根据周期性可得出f(2016)=f(504×4+0)=f(0)=0.
解答 解:∵f(x)是定义在R上的奇函数,
∴f(0)=0,
∵f(x+2)=-f(x),
∴f(x+4)=-f(x+2)=f(x),
∴f(x)的周期为4,
∴f(2016)=f(504×4+0)=f(0)=0,
故答案为0.
点评 考查了函数的奇偶性和函数的周期性.属于常规题型,应熟练掌握.

练习册系列答案
相关题目
3.已知a>0,且a≠1,下列函数中,在其定义域内是单调函数而且又是奇函数的是( )
| A. | y=sinax | B. | y=logax2 | C. | y=ax-a-x | D. | y=tanax |
8.复数z=a3-2a+(m+a)i(a≥0,m∈R)的实部大于虚部,则m的取值范围为( )
| A. | (-∞,-2) | B. | (-2,+∞) | C. | (-∞,0) | D. | (0,+∞) |
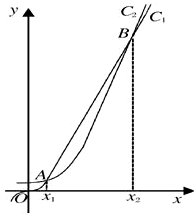 函数f(x)=2x和g(x)=x3的部分图象的示意图如图所示.设两函数的图象交于点A(x1,y1)、B(x2,y2),x1<x2.
函数f(x)=2x和g(x)=x3的部分图象的示意图如图所示.设两函数的图象交于点A(x1,y1)、B(x2,y2),x1<x2.