题目内容
13.如果复数z=$\frac{1+ai}{1+i}$(i为虚数单位)的实部与虚部互为相反数,那么|z|=$\frac{\sqrt{2}}{2}$.分析 利用复数的运算法则及其实部与虚部互为相反数,解得a,再利用复数模的计算公式即可得出.
解答 解:复数z=$\frac{1+ai}{1+i}$=$\frac{(1+ai)(1-i)}{(1+i)(1-i)}$=$\frac{1+a+(a-1)i}{2}$的实部与虚部互为相反数,
∴$\frac{1+a}{2}$+$\frac{a-1}{2}$=0,解得a=0.
∴z=$\frac{1}{2}-\frac{1}{2}i$.
∴|z|=$\sqrt{(\frac{1}{2})^{2}+(-\frac{1}{2})^{2}}$=$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查了复数的运算法则、实部与虚部的定义、相反数,、复数模的计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.设等差数列{an}的前n项和为Sn,若a1=1,S3=15,则S6=( )
| A. | 62 | B. | 66 | C. | 70 | D. | 74 |
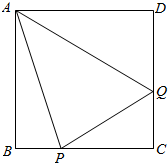 如图,某公司有一块边长为1百米的正方形空地ABCD,现要在正方形空地中规划一个三角形区域PAQ种植花草,其中P,Q分别为边BC,CD上的动点,∠PAQ=$\frac{π}{4}$,其它区域安装健身器材,设∠BAP为θ弧度.
如图,某公司有一块边长为1百米的正方形空地ABCD,现要在正方形空地中规划一个三角形区域PAQ种植花草,其中P,Q分别为边BC,CD上的动点,∠PAQ=$\frac{π}{4}$,其它区域安装健身器材,设∠BAP为θ弧度.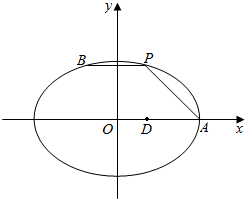 如图,在平面直角坐标系xOy中,已知点A为椭圆$\frac{{x}^{2}}{9}$+$\frac{2{y}^{2}}{9}$=1的右顶点,点D(1,0),点P,B在椭圆上,且在x轴上方,$\overrightarrow{BP}$=$\overrightarrow{DA}$.
如图,在平面直角坐标系xOy中,已知点A为椭圆$\frac{{x}^{2}}{9}$+$\frac{2{y}^{2}}{9}$=1的右顶点,点D(1,0),点P,B在椭圆上,且在x轴上方,$\overrightarrow{BP}$=$\overrightarrow{DA}$.