题目内容
已知函数f﹙x﹚=loga(1+x),g﹙x﹚=loga﹙x-1﹚﹙a>0且a≠1﹚.
①求函数f﹙x﹚+g﹙x﹚的定义域;
②判断函数f﹙x﹚+g﹙x﹚的奇偶性并说明理由;
③求使f﹙x﹚-g(2x)>0成立的x的集合.
①求函数f﹙x﹚+g﹙x﹚的定义域;
②判断函数f﹙x﹚+g﹙x﹚的奇偶性并说明理由;
③求使f﹙x﹚-g(2x)>0成立的x的集合.
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:①要使函数f﹙x﹚+g﹙x﹚有意义,需
,由此求得函数f﹙x﹚+g﹙x﹚的定义域.
②根据函数F(x)的定义域不关于原点对称,可得函数F(x)是非奇非偶函数.
③要解的不等式即loga(1+x)>loga(2x-1),分当a>1时 和当 0<a<1时两种情况,分别利用对数函数的定义域及单调性求得不等式的解集.
|
②根据函数F(x)的定义域不关于原点对称,可得函数F(x)是非奇非偶函数.
③要解的不等式即loga(1+x)>loga(2x-1),分当a>1时 和当 0<a<1时两种情况,分别利用对数函数的定义域及单调性求得不等式的解集.
解答:
解:①∵函数f﹙x﹚=loga(1+x),g﹙x﹚=loga﹙x-1﹚,
要使函数f﹙x﹚+g﹙x﹚有意义,需
,解得x>1,
故函数f﹙x﹚+g﹙x﹚的定义域为(1,+∞).
②令F(x)=f﹙x﹚+g﹙x﹚,则由①可得函数F(x)的定义域为(1,+∞),
不关于原点对称,故函数F(x)是非奇非偶函数.
③由f﹙x﹚-g(2x)>0可得 loga(1+x)>loga(2x-1),
当a>1时,不等式化为1+x>2x-1>0,解得
<x<2,故不等式的解集为(
,2);
当 0<a<1时,不等式化为2x-1>x+1>0,解得 x>2,故不等式的解集为(2,+∞).
要使函数f﹙x﹚+g﹙x﹚有意义,需
|
故函数f﹙x﹚+g﹙x﹚的定义域为(1,+∞).
②令F(x)=f﹙x﹚+g﹙x﹚,则由①可得函数F(x)的定义域为(1,+∞),
不关于原点对称,故函数F(x)是非奇非偶函数.
③由f﹙x﹚-g(2x)>0可得 loga(1+x)>loga(2x-1),
当a>1时,不等式化为1+x>2x-1>0,解得
| 1 |
| 2 |
| 1 |
| 2 |
当 0<a<1时,不等式化为2x-1>x+1>0,解得 x>2,故不等式的解集为(2,+∞).
点评:本题主要考查对数函数的图象和性质综合应用,对数不等式的解法,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目

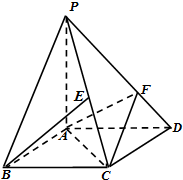 如图,四棱锥P-ABCD的底面ABCD是平行四边形,AD=2,AB=1,∠ABC=60°,PA⊥面ABCD,设E为PC中点,点F在线段PD上且PF=2FD.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,AD=2,AB=1,∠ABC=60°,PA⊥面ABCD,设E为PC中点,点F在线段PD上且PF=2FD. 某办公室共有6人,组织出门旅行,旅行车上的6个座位如图所示,其中甲、乙两人的关系较为亲密,要求在同一排且相邻,则不同的安排方法有
某办公室共有6人,组织出门旅行,旅行车上的6个座位如图所示,其中甲、乙两人的关系较为亲密,要求在同一排且相邻,则不同的安排方法有