题目内容
若x0是函数f(x)=2x+3x的零点,且x0∈(a,a+1),a∈Z,则a= .
考点:函数零点的判定定理
专题:函数的性质及应用
分析:函数零点左右两边函数值的符号相反,根据函数在一个区间上两个端点的函数值的符号确定是否存在零点.
解答:
解:由f(-1)=
-3<0,f(0)=1>0,及零点定理知f(x)的零点在区间(-1,0)上,
∴零点所在的一个区间是(a,a+1)=(-1,0)
∴a=-1,
故答案为:-1
| 1 |
| 2 |
∴零点所在的一个区间是(a,a+1)=(-1,0)
∴a=-1,
故答案为:-1
点评:本题主要考查函数零点的概念与零点定理的应用,本题的解题的关键是检验函数值的符号.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知焦点在x轴上的椭圆离心率e=
,它的半长轴长等于圆x2+y2-2x-3=0的半径,则椭圆的标准方程是( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知定义在R上的奇函数f(x),满足f(x+2)=-f(x),当c∈(0,2)时,f(x)=2x2,则f(7)=( )
| A、-2 | B、2 | C、98 | D、-98 |
已知数列{an}满足an=1+
+
+…+
,则ak+1-ak共有( )项.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n2 |
| A、1 | B、k | C、2k | D、2k+1 |
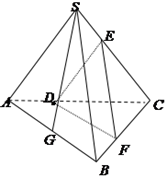 如图,在三棱锥S-ABC中,D、E、F分别是棱AC、BC、SC上的点,且CD=2DA,CE=2ES,CF=2FB,G是AB的中点.求证:SG∥平面DEF.
如图,在三棱锥S-ABC中,D、E、F分别是棱AC、BC、SC上的点,且CD=2DA,CE=2ES,CF=2FB,G是AB的中点.求证:SG∥平面DEF. 如图,用长为2的铁丝焊接成中部为矩形,两边为半圆形的框架,若半圆半径为x,求此框架围成的面积y与x的函数式y=f(x),写出它的定义域,并求出面积的最大值.
如图,用长为2的铁丝焊接成中部为矩形,两边为半圆形的框架,若半圆半径为x,求此框架围成的面积y与x的函数式y=f(x),写出它的定义域,并求出面积的最大值.